题目内容
20．
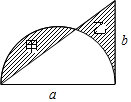如图，已知直角三角形的两条直角边分别为a、b，以a为直径画一个半圆．若甲、乙两阴影部分的面积相等，则用a的代数式表示b=$\frac{1}{4}$πa．
分析 根据已知条件得到S半圆=S直角三角形，列方程即可得到结论．
解答 解：∵甲、乙两阴影部分的面积相等，
∴S半圆=S直角三角形，
即$\frac{1}{2}×$（$\frac{1}{2}$a）2π=$\frac{1}{2}$ab，
∴b=$\frac{1}{4}$πa，
故答案为：$\frac{1}{4}$πa．
点评 本题考查了扇形的面积的计算，三角形面积的计算，推出S半圆=S直角三角形是解题的关键．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
10．
等腰△ABC中，AB=AC，D为底边BC的中点，E为底边上一动点，过E分别向AB，AC作垂线段垂足F，G．连DF，DG．证明：DF=DG，∠EFD=∠EGD，∠FDG=∠FEG=180°-∠A．
等腰△ABC中，AB=AC，D为底边BC的中点，E为底边上一动点，过E分别向AB，AC作垂线段垂足F，G．连DF，DG．证明：DF=DG，∠EFD=∠EGD，∠FDG=∠FEG=180°-∠A． 
如图，点O是原点，AB∥x轴，点M在线段AB上，且OM=2b，点E是线段AO的中点，若点B和点E关于直线OM对称，点B的坐标是（0，a），则点A的坐标是（3b，a） （结果用a，b表示）．
如图，已知△ABC是等边三角形，点B、C、D在同一直线上，点E在AC上，且CE=CD，则∠D=30°．
15．在代数式：$\frac{ab}{3}$，-$\frac{2}{3}$abc，0，-5a，x-y，$\frac{2}{x}$，$\frac{1}{π}$中，单项式有（ ）
| A． | 6个 | B． | 5个 | C． | 4个 | D． | 3个 |
12．已知一次函数y=$\frac{3}{2}$x+a与y=-$\frac{1}{2}$x+b的图象都经过点A（-2，0），且与y轴分别交于B，C两点，那么△ABC的面积是（ ）
| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
7．
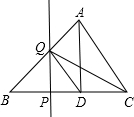如图，△ABC中，AD⊥BC，垂足为D，AD=BD=3，CD=2，点P从点B出发沿线段BC的方向移动到点C停止，过点P作PQ⊥BC，交折线BA-AC于点Q，连接DQ、CQ，若△ADQ与△CDQ的面积相等，则线段BP的长度是（ ）
如图，△ABC中，AD⊥BC，垂足为D，AD=BD=3，CD=2，点P从点B出发沿线段BC的方向移动到点C停止，过点P作PQ⊥BC，交折线BA-AC于点Q，连接DQ、CQ，若△ADQ与△CDQ的面积相等，则线段BP的长度是（ ）| A． | $\frac{9}{5}$或4 | B． | $\frac{6}{5}$或4 | C． | $\frac{9}{5}$或$\frac{13}{5}$ | D． | $\frac{6}{5}$或$\frac{13}{5}$ |