题目内容
12.已知一次函数y=$\frac{3}{2}$x+a与y=-$\frac{1}{2}$x+b的图象都经过点A(-2,0),且与y轴分别交于B,C两点,那么△ABC的面积是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 可先根据点A的坐标用待定系数法求出a,b的值,即求出两个一次函数的解析式,进而求出它们与y轴的交点,即B,C的坐标.那么三角形ABC中,底边的长应该是B,C纵坐标差的绝对值,高就应该是A点横坐标的绝对值,因此可根据三角形的面积公式求出三角形的面积.
解答 解:把点A(-2,0)代入y=$\frac{3}{2}$x+a,
得:a=3,
∴点B(0,3).
把点A(-2,0)代入y=-$\frac{1}{2}$x+b,
得:b=-1,
∴点C(0,-1).
∴BC=|3-(-1)|=4,
∴S△ABC=$\frac{1}{2}$×2×4=4.
故选C.
点评 本题考查了用待定系数法求函数解析式以及一次函数与方程的关系,通过已知点的坐标来得出两函数的解析式是解题的关键.

练习册系列答案
相关题目
7.一只蚂蚁从数轴表示数-2的点A出发,向右直爬5个单位到达点B,则点B所表示的数为( )
| A. | 5 | B. | 3 | C. | -3 | D. | -1 |
4.一元二次方程2x2+x-3=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 没有实数根 | D. | 无法确定 |
1.有一人患了流感,经过两轮传染后共有64人患了流感.设每轮传染中平均一个人传染了x个人,列出的方程是( )
| A. | x(x+1)=64 | B. | x(x-1)=64 | C. | (1+x)2=64 | D. | (1+2x)=64 |
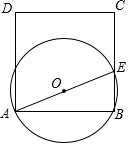 如图,正方形ABCD的边长为1,点E为BC边上一动点,以AE为直径作⊙O.
如图,正方形ABCD的边长为1,点E为BC边上一动点,以AE为直径作⊙O.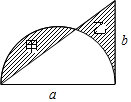 如图,已知直角三角形的两条直角边分别为a、b,以a为直径画一个半圆.若甲、乙两阴影部分的面积相等,则用a的代数式表示b=$\frac{1}{4}$πa.
如图,已知直角三角形的两条直角边分别为a、b,以a为直径画一个半圆.若甲、乙两阴影部分的面积相等,则用a的代数式表示b=$\frac{1}{4}$πa.