题目内容
11. 如图,点O是原点,AB∥x轴,点M在线段AB上,且OM=2b,点E是线段AO的中点,若点B和点E关于直线OM对称,点B的坐标是(0,a),则点A的坐标是(3b,a) (结果用a,b表示).
如图,点O是原点,AB∥x轴,点M在线段AB上,且OM=2b,点E是线段AO的中点,若点B和点E关于直线OM对称,点B的坐标是(0,a),则点A的坐标是(3b,a) (结果用a,b表示).
分析 根据点B的坐标求出OB的长,再连接ME,根据轴对称的性质可得OB=OE,再求出AO的长度,然后利用三角函数得到∠A=30°,∠AOB=60°,进一步得到∠BOM=∠AOM=30°,再根据等角对等边得到AM=OM=2b,根据三角函数得到BM=$\frac{1}{2}$OM=b,从而求出AB的长,然后写出点A的坐标即可.
解答 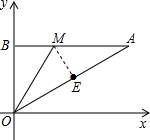 解:∵点B(0,a),
解:∵点B(0,a),
∴OB=a,
连接ME,
∵点B和点E关于直线OM对称,
∴OB=OE=a,
∵点E是线段AO的中点,
∴AO=2OE=2a,
∴∠A=30°,∠AOB=60°,
∴∠BOM=∠AOM=30°,
∴AM=OM=2b,
∵BM=$\frac{1}{2}$OM=b,
∴AB=BM+MA=3a,
∴点A的坐标是(3b,a).
故答案为:(3b,a).
点评 本题考查了轴对称的性质,坐标与图形性质,解直角三角形,熟练掌握轴对称的性质并作出辅助线构造出直角三角形是解题的关键.

练习册系列答案
相关题目
19.已知y是x的正比例函数,x是z的反比例函数,则( )
| A. | y是z的正比例函数 | B. | y是z的反比例函数 | ||
| C. | y是z的函数但不一定是反比例函数 | D. | y是z的函数但不一定是正比例函数 |
6. 如图,OA,OB是⊙O的半径,点C在⊙O上,连接AC,BC,若∠A=20°,∠B=70°,则∠ACB的度数为 ( )
如图,OA,OB是⊙O的半径,点C在⊙O上,连接AC,BC,若∠A=20°,∠B=70°,则∠ACB的度数为 ( )
 如图,OA,OB是⊙O的半径,点C在⊙O上,连接AC,BC,若∠A=20°,∠B=70°,则∠ACB的度数为 ( )
如图,OA,OB是⊙O的半径,点C在⊙O上,连接AC,BC,若∠A=20°,∠B=70°,则∠ACB的度数为 ( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
16.2015年我国的国民生产总值约为1300800亿元,那么1300800用科学记数法表示正确的是( )
| A. | 1.3008×106 | B. | 13.008×105 | C. | 1.3008×104 | D. | 0.13008×107 |
1.有一人患了流感,经过两轮传染后共有64人患了流感.设每轮传染中平均一个人传染了x个人,列出的方程是( )
| A. | x(x+1)=64 | B. | x(x-1)=64 | C. | (1+x)2=64 | D. | (1+2x)=64 |
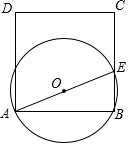 如图,正方形ABCD的边长为1,点E为BC边上一动点,以AE为直径作⊙O.
如图,正方形ABCD的边长为1,点E为BC边上一动点,以AE为直径作⊙O.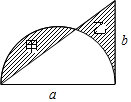 如图,已知直角三角形的两条直角边分别为a、b,以a为直径画一个半圆.若甲、乙两阴影部分的面积相等,则用a的代数式表示b=$\frac{1}{4}$πa.
如图,已知直角三角形的两条直角边分别为a、b,以a为直径画一个半圆.若甲、乙两阴影部分的面积相等,则用a的代数式表示b=$\frac{1}{4}$πa.