题目内容
13.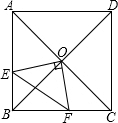 在正方形ABCD中,O是对角线的交点,过O作OE⊥OF,分别交AB,BC于E,F,若AE=4,CF=3.
在正方形ABCD中,O是对角线的交点,过O作OE⊥OF,分别交AB,BC于E,F,若AE=4,CF=3.(1)求证:△BOE≌△COF;
(2)求EF的长和四边形OEBF的面积.
分析 (1)由正方形的性质得出OB=OC=OA=OD,∠BAD=∠ABC=∠BCD=90°,∠OBE=∠OCF=45°,证出∠BOE=∠COF,由ASA证明△BOE≌△COF即可;
(2)由全等三角形的性质得出BE=CF=3,同理△AOE≌△BOF,得出BF=AE=4,AB=7,由勾股定理求出EF;由全等三角形的性质得出四边形OEBF的面积=△AOB的面积=$\frac{1}{4}$正方形ABCD的面积,即可得出结果.
解答 (1)证明:∵四边形ABCD是正方形,
∴OB=OC=OA=OD,∠BAD=∠ABC=∠BCD=90°,∠OBE=∠OCF=45°,AC⊥BD,
∴∠BOC=90°,
∵OE⊥OF,
∴∠EOF=90°,
∴∠BOE=∠COF,
在△BOE和△COF中,$\left\{\begin{array}{l}{∠BOE=∠COF}&{\;}\\{OB=OC}&{\;}\\{∠OBE=∠OCF}&{\;}\end{array}\right.$,
∴△BOE≌△COF(ASA);
(2)解:∵△BOE≌△COF,
∴BE=CF=3,
同理:△AOE≌△BOF,
∴BF=AE=4,
∴AB=AE+BE=7,EF=$\sqrt{B{E}^{2}+B{F}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5;
∵△BOE≌△COF,△AOE≌△BOF,
∴四边形OEBF的面积=△BOE的面积+△AOE的面积
=△AOB的面积=$\frac{1}{4}$正方形ABCD的面积
=$\frac{1}{4}$×72=$\frac{49}{4}$.
点评 本题考查了正方形的性质、全等三角形的判定与性质、勾股定理;熟练掌握正方形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
9.八年级一、二班举行投篮比赛,每班各挑选10名同学代表班级共参加5场投篮比赛,投篮得分如下:
(1)一班得分的中位数与二班得分的众数分别是多少?
(2)分别求出两个班五场比赛得分的平均值;
(3)你认为哪个班级的得分较稳定?为什么?
| 场次 得分 班级 | 1 | 2 | 3 | 4 | 5 |
| 一班 | 85 | 88 | 77 | 75 | 85 |
| 二班 | 95 | 85 | 70 | 80 | 80 |
(2)分别求出两个班五场比赛得分的平均值;
(3)你认为哪个班级的得分较稳定?为什么?
8.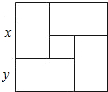 用四个完全一样的长方形和一个小正方形拼成如图所示的大长方形的长和宽,已知大正方形的面积是121,小正方形的面积是9,若用x,y(x>y)表示长方形的长和宽,则下列关系中不正确的是( )
用四个完全一样的长方形和一个小正方形拼成如图所示的大长方形的长和宽,已知大正方形的面积是121,小正方形的面积是9,若用x,y(x>y)表示长方形的长和宽,则下列关系中不正确的是( )
 用四个完全一样的长方形和一个小正方形拼成如图所示的大长方形的长和宽,已知大正方形的面积是121,小正方形的面积是9,若用x,y(x>y)表示长方形的长和宽,则下列关系中不正确的是( )
用四个完全一样的长方形和一个小正方形拼成如图所示的大长方形的长和宽,已知大正方形的面积是121,小正方形的面积是9,若用x,y(x>y)表示长方形的长和宽,则下列关系中不正确的是( )| A. | x+y=11 | B. | x2+y2=180 | C. | x-y=3 | D. | x•y=28 |
3. 如图,能判断直线AB∥CD的条件是( )
如图,能判断直线AB∥CD的条件是( )
 如图,能判断直线AB∥CD的条件是( )
如图,能判断直线AB∥CD的条件是( )| A. | ∠1=∠2 | B. | ∠1+∠3=180° | C. | ∠3=∠4 | D. | ∠3+∠4=180° |
 如图,将面积为a2的正方形ADGF与面积为b2的正方形BGCE放在一起(b>a>0),试用a、b表示三角形ABC的面积.
如图,将面积为a2的正方形ADGF与面积为b2的正方形BGCE放在一起(b>a>0),试用a、b表示三角形ABC的面积. 如图,在矩形ABCD中,AB=8,BC=6,将矩形沿EF折叠,使顶点B与D重合,则折痕EF的长为7.5.
如图,在矩形ABCD中,AB=8,BC=6,将矩形沿EF折叠,使顶点B与D重合,则折痕EF的长为7.5.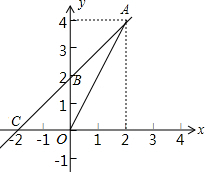 如图,一次函数y=kx+b的图象经过(2,4)、(0,2)两点,与x轴相交于点C.求:
如图,一次函数y=kx+b的图象经过(2,4)、(0,2)两点,与x轴相交于点C.求: 如图,一个正方体的棱长为2cm,一只蚂蚁欲从A点处沿正方体侧面到B点处吃食物,那么它需要爬行的最短路径的长是2$\sqrt{5}$cm.
如图,一个正方体的棱长为2cm,一只蚂蚁欲从A点处沿正方体侧面到B点处吃食物,那么它需要爬行的最短路径的长是2$\sqrt{5}$cm.