题目内容
8.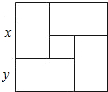 用四个完全一样的长方形和一个小正方形拼成如图所示的大长方形的长和宽,已知大正方形的面积是121,小正方形的面积是9,若用x,y(x>y)表示长方形的长和宽,则下列关系中不正确的是( )
用四个完全一样的长方形和一个小正方形拼成如图所示的大长方形的长和宽,已知大正方形的面积是121,小正方形的面积是9,若用x,y(x>y)表示长方形的长和宽,则下列关系中不正确的是( )| A. | x+y=11 | B. | x2+y2=180 | C. | x-y=3 | D. | x•y=28 |
分析 根据大正方形及小正方形的面积,分别求出大正方形及小正方形的边长,然后解出x、y的值,即可判断各选项.
解答 解:由题意得,大正方形的边长为14,小正方形的边长为2
∴x+y=11,x-y=3,
则$\left\{\begin{array}{l}{x+y=11}\\{x-y=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=7}\\{y=4}\end{array}\right.$.
故可得B选项的关系式不正确.
故选:B.
点评 此题考查了二元一次方程组的应用,解答本题的关键是根据大正方形的边长及小正方形的边长,结合图形建立方程组,进一步解决问题.

练习册系列答案
相关题目
4.一个多边形的内角和与外角和相差180°,则这个多边形是( )
| A. | 三角形 | B. | 五边形 | C. | 三角形或五边形 | D. | 三角形或六边形 |
18.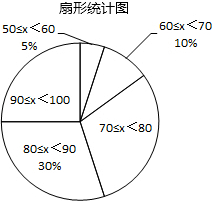 某校组织初中2000名学生游览参观“五大道”,并以此开展“五大道”历史经历知识竞赛活动,现从中随机抽取若干名学生的得分(满分100分,成绩均为正数)进行统计,整理出下列竞赛成绩统计表和扇形统计图(均不完整).
某校组织初中2000名学生游览参观“五大道”,并以此开展“五大道”历史经历知识竞赛活动,现从中随机抽取若干名学生的得分(满分100分,成绩均为正数)进行统计,整理出下列竞赛成绩统计表和扇形统计图(均不完整).
成绩统计表
如果成绩在90分以上(含90分)可获得一等奖;70分以上(含70分),90分以下的可获得二等奖;其余学生可获得鼓励奖,根据以上图表的数据解答下列问题:
(1)本次活动共随机抽取了多少名学生?
(2)估计本次活动获得二等奖的学生有多少名?
(3)绘制频数分布直方图.
 某校组织初中2000名学生游览参观“五大道”,并以此开展“五大道”历史经历知识竞赛活动,现从中随机抽取若干名学生的得分(满分100分,成绩均为正数)进行统计,整理出下列竞赛成绩统计表和扇形统计图(均不完整).
某校组织初中2000名学生游览参观“五大道”,并以此开展“五大道”历史经历知识竞赛活动,现从中随机抽取若干名学生的得分(满分100分,成绩均为正数)进行统计,整理出下列竞赛成绩统计表和扇形统计图(均不完整).成绩统计表
| 成绩x(分) | 频数(人) |
| 50≤x<60 | 10 |
| 60≤x<70 | 20 |
| 70≤x<80 | 60 |
| 80≤x<90 | 60 |
| 90≤x<100 | 50 |
(1)本次活动共随机抽取了多少名学生?
(2)估计本次活动获得二等奖的学生有多少名?
(3)绘制频数分布直方图.
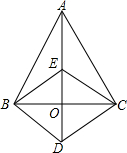 如图,△ABC中,O是边BC的中点,点D是AD延长线上一点,BE∥CD交AD于E,连接BD、CE
如图,△ABC中,O是边BC的中点,点D是AD延长线上一点,BE∥CD交AD于E,连接BD、CE
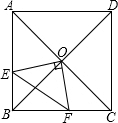 在正方形ABCD中,O是对角线的交点,过O作OE⊥OF,分别交AB,BC于E,F,若AE=4,CF=3.
在正方形ABCD中,O是对角线的交点,过O作OE⊥OF,分别交AB,BC于E,F,若AE=4,CF=3.
 如图,已知AB=AC,AD=AE,BD=EC,则图中有2对全等三角形,它们是△ABD≌△ACE,△ABE≌△ACD.
如图,已知AB=AC,AD=AE,BD=EC,则图中有2对全等三角形,它们是△ABD≌△ACE,△ABE≌△ACD.