题目内容
10. 如图,将面积为a2的正方形ADGF与面积为b2的正方形BGCE放在一起(b>a>0),试用a、b表示三角形ABC的面积.
如图,将面积为a2的正方形ADGF与面积为b2的正方形BGCE放在一起(b>a>0),试用a、b表示三角形ABC的面积.
分析 阴影部分面积等于梯形ADGB的面积加上三角形BGC的面积减去三角形ADC的面积,由此代入字母求得结论即可.
解答 解:∵面积为a2的正方形ADGF与面积为b2的正方形BGCE放在一起(b>a>0),
∴正方形ADGF的边长为a,正方形BGCE为b,
∴S阴影=S梯形ADGB+S△BGC-S△ADC
=$\frac{1}{2}$a(a+b)+$\frac{1}{2}$b2-$\frac{1}{2}$a(a+b)
=$\frac{1}{2}$b2,
即三角形ABC的面积是$\frac{1}{2}$b2.
点评 此题考查列代数式,利用基本图形的面积的和与差表示出阴影部分面积是解决问题的关键.

练习册系列答案
相关题目
20. 某教育部门为了解全市七年级学生对数学知识的掌握情况,在一次数学检测中,从全市七年级考生中随机抽取200名学生的数学成绩进行调查,并将调查结果绘制成如图表:
某教育部门为了解全市七年级学生对数学知识的掌握情况,在一次数学检测中,从全市七年级考生中随机抽取200名学生的数学成绩进行调查,并将调查结果绘制成如图表:
请根据图表提供的信息,解答下列问题:
(1)请求出a的值,并补全下列条形统计图;
(2)如果90分以上的为优秀,请你根据抽取的样本情况估计某市九年级同学在本次数学检测中的优秀率.
 某教育部门为了解全市七年级学生对数学知识的掌握情况,在一次数学检测中,从全市七年级考生中随机抽取200名学生的数学成绩进行调查,并将调查结果绘制成如图表:
某教育部门为了解全市七年级学生对数学知识的掌握情况,在一次数学检测中,从全市七年级考生中随机抽取200名学生的数学成绩进行调查,并将调查结果绘制成如图表:请根据图表提供的信息,解答下列问题:
| 分数段 | 人数 |
| x<60 | 20 |
| 60≤x<70 | 28 |
| 70≤x<80 | 54 |
| 80≤x<90 | a |
| 90≤x<100 | 24 |
| 100≤x<110 | 18 |
| 110≤x≤120 | 16 |
(2)如果90分以上的为优秀,请你根据抽取的样本情况估计某市九年级同学在本次数学检测中的优秀率.
14.如图中,表示函数关系的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,AB∥CD且∠1=∠2,问AM与CN是否平行?为什么?
如图,AB∥CD且∠1=∠2,问AM与CN是否平行?为什么? 已知AB∥CD,∠BEF=∠BFE,∠DEG=∠DGE,你能判断EG与EF的位置关系吗?说明你的理由.
已知AB∥CD,∠BEF=∠BFE,∠DEG=∠DGE,你能判断EG与EF的位置关系吗?说明你的理由.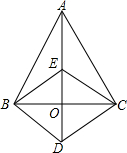 如图,△ABC中,O是边BC的中点,点D是AD延长线上一点,BE∥CD交AD于E,连接BD、CE
如图,△ABC中,O是边BC的中点,点D是AD延长线上一点,BE∥CD交AD于E,连接BD、CE 已知,如图,∠A=∠1,∠E=∠2,AC⊥EC,试说明AB∥DE的理由.
已知,如图,∠A=∠1,∠E=∠2,AC⊥EC,试说明AB∥DE的理由.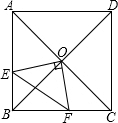 在正方形ABCD中,O是对角线的交点,过O作OE⊥OF,分别交AB,BC于E,F,若AE=4,CF=3.
在正方形ABCD中,O是对角线的交点,过O作OE⊥OF,分别交AB,BC于E,F,若AE=4,CF=3.