题目内容
3．观察下列各式：（x-1）（x+1）=x2-1，（x-1）（x2+x+1）=x3-1，（x-1）（x3+x2+x+1）=x4-1…（1）根据以上规律，可得（x-1）（x6+x5+x4+x3+x2+x+1）=x7-1；
（2）计算：210+29+28+27+26+25+24+23+22+2+1．
分析 （1）根据已知等式得出一般性规律，即可得到结果；
（2）原式变形后，利用得出的规律计算即可得到结果．
解答 解：（1）（x-1）（x6+x5+x4+x3+x2+x+1）=x7-1；
故答案为：x7-1；
（2）原式=（2-1）•（210+29+…+22+2+1）=211-1=2047．
点评 此题考查了多项式乘以多项式，弄清题中的规律是解本题的关键．
练习册系列答案
相关题目
如图，BD平分∠ABC，DA⊥AB，∠1=55°，∠2=85°，求∠C的度数．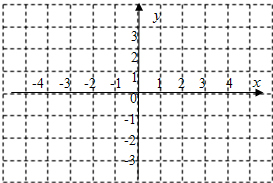
如图，方格纸中每个小方格都是边长为1个单位长度的正方形，已知点A（-1，1），现将A点先向左平移3个单位，再向下平移4个单位得到点B，然后作点B关于y轴的对称点得到C点，最后做点C关于x轴的对称点得到D点．