题目内容
12.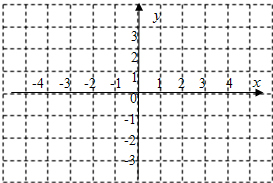 如图,方格纸中每个小方格都是边长为1个单位长度的正方形,已知点A(-1,1),现将A点先向左平移3个单位,再向下平移4个单位得到点B,然后作点B关于y轴的对称点得到C点,最后做点C关于x轴的对称点得到D点.
如图,方格纸中每个小方格都是边长为1个单位长度的正方形,已知点A(-1,1),现将A点先向左平移3个单位,再向下平移4个单位得到点B,然后作点B关于y轴的对称点得到C点,最后做点C关于x轴的对称点得到D点.(1)在坐标系中作出点A、B、C、D;
(2)顺次连接ABCDA,求四边形ABCD的面积.
分析 (1)首先在坐标系中作出点A,再根据平移的性质得出B的坐标,利用关于x轴、y轴对称的点的坐标特征求出C、D的坐标;
(2)作AE⊥BC于E.根据四边形ABCD的面积=△ABE的面积+梯形AECD的面积即可求解.
解答  解:(1)如图所示:
解:(1)如图所示:
(2)如图,作AE⊥BC于E.
四边形ABCD的面积=△ABE的面积+梯形AECD的面积
=$\frac{1}{2}$×3×4+$\frac{1}{2}$×(4+6)×5
=6+25
=31.
点评 本题考查了坐标与图形变化-平移,关于x轴、y轴对称的点的坐标,坐标与图形性质,四边形的面积.用到的知识点:
平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数.即点P(x,y)关于x轴的对称点P′的坐标是(x,-y).
关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变.即点P(x,y)关于y轴的对称点P′的坐标是(-x,y).

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
2. 如图,若点M是线段AC的中点,N是线段BC的中点,且AB=8,CN=1.5,则AM=( )
如图,若点M是线段AC的中点,N是线段BC的中点,且AB=8,CN=1.5,则AM=( )
 如图,若点M是线段AC的中点,N是线段BC的中点,且AB=8,CN=1.5,则AM=( )
如图,若点M是线段AC的中点,N是线段BC的中点,且AB=8,CN=1.5,则AM=( )| A. | 2 | B. | 3 | C. | 2.5 | D. | 1.5 |
 求直线y=2x+4和y=-3x+9与x轴所围成三角形的面积.
求直线y=2x+4和y=-3x+9与x轴所围成三角形的面积.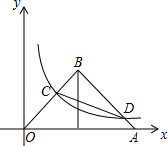 如图,△OAB是等要直角三角形,∠B=90°,BO=BA,OA=4,点O是坐标原点,点A在x轴的正半轴上,双曲线y=$\frac{k}{x}$过OB的中点C且与AB交于点D,连接CD,则∠BDC=30°.
如图,△OAB是等要直角三角形,∠B=90°,BO=BA,OA=4,点O是坐标原点,点A在x轴的正半轴上,双曲线y=$\frac{k}{x}$过OB的中点C且与AB交于点D,连接CD,则∠BDC=30°.