题目内容
5.若一次函数y=-x${\;}^{{m}^{2}-8}$+m-2的图象经过第三象限,则m=-3.分析 根据一次函数的定义及函数图象经过第三象限列出关于m的不等式组,求出m的值即可.
解答 解:∵一次函数y=-x${\;}^{{m}^{2}-8}$+m-2的图象经过第三象限,
∴$\left\{\begin{array}{l}{m}^{2}-8=1\\ m-2<0\end{array}\right.$,解得m=-3.
故答案为:-3.
点评 本题考查的是一次函数的图象与系数的关系,熟知一次函数y=kx+b(k≠0)中,当k<0,b<0时函数的图象在二、三、四象限是解答此题的关键.

练习册系列答案
相关题目
13.反比例函数y=$\frac{k}{x}$的图象经过点A(-2,-5),则当1<x<2时,y的取值范围是( )
| A. | -10<y<-5 | B. | -2<y<-1 | C. | 5<y<10 | D. | y>10 |
14.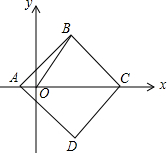 如图,在平面直角坐标系中,O为坐标原点,正方形ABCD的对角线AC落在x轴上,A(-1,0),C(7,0),连接OB,则∠BOC的正弦值为( )
如图,在平面直角坐标系中,O为坐标原点,正方形ABCD的对角线AC落在x轴上,A(-1,0),C(7,0),连接OB,则∠BOC的正弦值为( )
 如图,在平面直角坐标系中,O为坐标原点,正方形ABCD的对角线AC落在x轴上,A(-1,0),C(7,0),连接OB,则∠BOC的正弦值为( )
如图,在平面直角坐标系中,O为坐标原点,正方形ABCD的对角线AC落在x轴上,A(-1,0),C(7,0),连接OB,则∠BOC的正弦值为( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
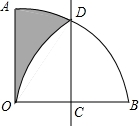 如图,扇形AOB的圆心角为90°,半径为2,点C为OB中点,点D在$\widehat{AB}$上,将扇形沿直线CD折叠,若点B,O重合,则图中阴影部分的周长为π+2.(结果保留π)
如图,扇形AOB的圆心角为90°,半径为2,点C为OB中点,点D在$\widehat{AB}$上,将扇形沿直线CD折叠,若点B,O重合,则图中阴影部分的周长为π+2.(结果保留π)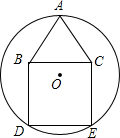 已知,如图等边三角形ABC和正方形BDEC的边长均为2,⊙O经过点A,D,E三点.
已知,如图等边三角形ABC和正方形BDEC的边长均为2,⊙O经过点A,D,E三点.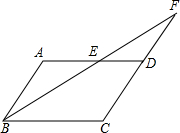 如图,在?ABCD中,AB=4,AD=7,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF的长是( )
如图,在?ABCD中,AB=4,AD=7,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF的长是( )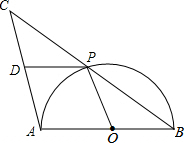 如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.
如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.