题目内容
13．已知方程3x2-x-1=0的两根为x1，x2．不解方程，求下列代数式的值．（1）（x1-1）（x2-1）；
（2）x1-x2．
分析 根据根与系数的关系得到x1+x2=$\frac{1}{3}$，x1x2=-$\frac{1}{3}$，
（1）利用乘法公式展开得到原式=x1x2-（x1+x2）+1，然后利用整体代入的方法计算；
（2）利用完全平方公式变形得到原式原式=±$\sqrt{（{x}_{1}+{x}_{2}）^{2}-4{x}_{1}{x}_{2}}$，然后利用整体代入的方法计算．
解答 解：根据题意得x1+x2=$\frac{1}{3}$，x1x2=-$\frac{1}{3}$，
（1）原式=x1x2-（x1+x2）+1=-$\frac{1}{3}$-$\frac{1}{3}$+1=$\frac{1}{3}$；
（2）原式=±$\sqrt{（{x}_{1}-{x}_{2}）^{2}}$=±$\sqrt{（{x}_{1}+{x}_{2}）^{2}-4{x}_{1}{x}_{2}}$=±$\sqrt{（\frac{1}{3}）^{2}-4×（-\frac{1}{3}）}$=±$\frac{\sqrt{13}}{3}$．
点评 本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．
练习册系列答案
孟建平名校考卷系列答案
相关题目
3．关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根，则k的取值范围是（ ）
| A． | k＞-1 | B． | k＜1 | C． | k＞-1且k≠0 | D． | k＜1且k≠0 |
4．一元二次方程-2x2+x-7=0的根的情况是（ ）
| A． | 没有实数根 | B． | 有两个相等的实数根 | ||
| C． | 有两个不相等的实数根 | D． | 无法确定 |
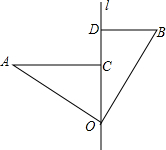如图，∠AOB=90°，OA=OB，直线l经过点O，分别过A、B两点作AC⊥l交l于点C，BD⊥l交l于点D．已知AC=6，BD=4，则CD=2．
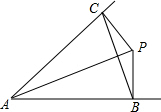如图，在△PBC中，∠PCB=∠PBC，若PC⊥AC，PB⊥AB，求证：∠PAC=$\frac{1}{2}$∠BAC．