题目内容
3.关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根,则k的取值范围是( )| A. | k>-1 | B. | k<1 | C. | k>-1且k≠0 | D. | k<1且k≠0 |
分析 根据一元二次方程的定义和△的意义得到k≠0且△>0,即(-2)2-4×k×(-1)>0,然后解不等式即可得到k的取值范围.
解答 解:∵关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根,
∴k≠0且△>0,即(-2)2-4×k×(-1)>0,
解得k>-1且k≠0.
故选C.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的定义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.为丰富学生课外活动,某校积极开展社团活动,学生科根据自己的爱好选择一项,已知该校开设的体育社团有:A:篮球,B:排球,C:足球,D:羽毛球,E:乒乓球,李老师对某年级同学选择体育社团的情况进行调查统计,制成了两幅不完整的统计图(如图).则以下结论正确的是( )
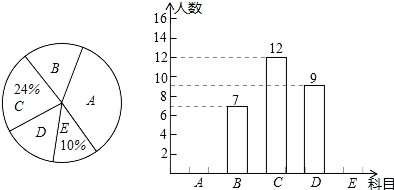

| A. | 选科目E的有10人 | |
| B. | 选科目B的扇形圆心角比选科目D的扇形圆心角的度数多14.4° | |
| C. | 选科目A、B的人数占选体育社团人数的一半 | |
| D. | 选科目A的占34% |
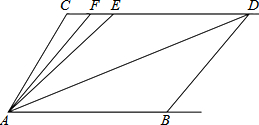 如图,已知射线CD∥AB,∠C=∠ABD=110°,E,F在CD上,且满足∠EAD=∠EDA,AF平分∠CAE.
如图,已知射线CD∥AB,∠C=∠ABD=110°,E,F在CD上,且满足∠EAD=∠EDA,AF平分∠CAE.