题目内容
1.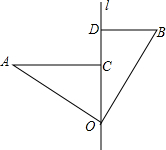 如图,∠AOB=90°,OA=OB,直线l经过点O,分别过A、B两点作AC⊥l交l于点C,BD⊥l交l于点D.已知AC=6,BD=4,则CD=2.
如图,∠AOB=90°,OA=OB,直线l经过点O,分别过A、B两点作AC⊥l交l于点C,BD⊥l交l于点D.已知AC=6,BD=4,则CD=2.
分析 根据同角的余角相等求出∠A=∠BOD,然后利用“角角边”证明△AOC和△OBD全等,根据全等三角形对应边相等推知AC=OD,OC=BD,则CD=OD-OC.
解答 解:∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∵AC⊥l,BD⊥l,
∴∠ACO=∠BDO=90°,
∴∠A+∠AOC=90°,
∴∠A=∠BOD,
在△AOC和△OBD中,
$\left\{\begin{array}{l}{∠A=∠BOD}\\{∠ACO=∠BDO}\\{OA=OB}\end{array}\right.$,
∴△AOC≌△OBD(AAS),
∴AC=OD=6,OC=BD=5,则CD=OD-OC=2.
故答案是:2.
点评 本题考查了全等三角形的判定与性质,同角的余角相等的性质,利用三角形全等证明边相等是常用的方法之一,要熟练掌握并灵活运用.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
10. 如图,BC:AB=1:2,延长AB到点B,使AB1=2AB,延长AC到点C1,使AC1=2AC,则sin∠AB1C1的值是( )
如图,BC:AB=1:2,延长AB到点B,使AB1=2AB,延长AC到点C1,使AC1=2AC,则sin∠AB1C1的值是( )
 如图,BC:AB=1:2,延长AB到点B,使AB1=2AB,延长AC到点C1,使AC1=2AC,则sin∠AB1C1的值是( )
如图,BC:AB=1:2,延长AB到点B,使AB1=2AB,延长AC到点C1,使AC1=2AC,则sin∠AB1C1的值是( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 无法判断 |
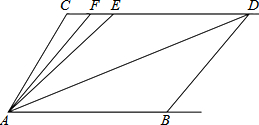 如图,已知射线CD∥AB,∠C=∠ABD=110°,E,F在CD上,且满足∠EAD=∠EDA,AF平分∠CAE.
如图,已知射线CD∥AB,∠C=∠ABD=110°,E,F在CD上,且满足∠EAD=∠EDA,AF平分∠CAE.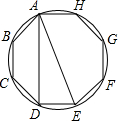 如图,正八边形ABCDEFGH内接于⊙O,则∠DAE的度数是22.5.
如图,正八边形ABCDEFGH内接于⊙O,则∠DAE的度数是22.5.