题目内容

12．已知一次函数y=kx+b，当x减少3时，y增加2，则k的值是-$\frac{2}{3}$．

分析 求出函数的解析式，再根据题意解答．

解答 解：由题意可得：$\left\{\begin{array}{l}{y=kx+b}\\{y+2=k（x-3）+b}\end{array}\right.$，
解得：k=-$\frac{2}{3}$，
故答案为：-$\frac{2}{3}$

点评 本题考查了用代定系数法求函数的解析式，关键是根据题意解答．

练习册系列答案
相关题目
2．已知，抛物线y=x2-2x+3与直线y=2x相交于A、B，抛物线与y轴相交于C点，求：△ABC的面积．
3．若x2-$\sqrt{5}$x+1=0，则x4+x-4=7．
20．解下列方程组
（1）$\left\{{\begin{array}{l}{x-2y=0}\\{3x+2y=8}\end{array}}\right.$
（2）$\left\{\begin{array}{l}2x+y=3\\ 3x-5y=11\end{array}\right.$
（3）$\left\{\begin{array}{l}\frac{m}{3}+\frac{n}{6}=2\\ \frac{m}{4}+\frac{n}{4}=2\end{array}\right.$
（4）$\left\{\begin{array}{l}3x+2y=5x+2\\ 2（3x+2y）=2x+8\end{array}\right.$
（5）$\left\{\begin{array}{l}{4（x-y-1）=3（1-y）-2}\\{\frac{x}{2}+\frac{y}{3}=2}\end{array}\right.$．
7．下列说法中错误的是（　　）
A．不等式x＜2的正整数解只有一个B．x＜$\frac{1}{2}$是不等式2x-1＜0的解集
C．不等式ax＞9的解集是x＞$\frac{9}{a}$D．不等式x＜10的整数解有无数个
17．若圆的一条弦长为12，其弦心距等于8，则该圆的半径等于10．
4．（1）求不等式组$\left\{\begin{array}{l}{x-1≥1-x}\\{x+8＞4x-1}\end{array}\right.$的整数解； 
（2）解方程：$\frac{x}{x-2}$-1=$\frac{1}{{x}^{2}-4}$．
1．设a，b是有理数，且满足a+$\sqrt{2}$b=${（1-\sqrt{2}）}^{2}$+$\sqrt{2}$，求$\root{a}{b}$的值．
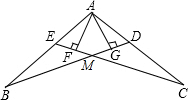2．如图，AB=AC，点D，E分别在AC、AB上，AG⊥BD于G，AF⊥CE于F，且AG=AF．求证：BD=CE．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网