题目内容
2. 已知,抛物线y=x2-2x+3与直线y=2x相交于A、B,抛物线与y轴相交于C点,求:△ABC的面积.
已知,抛物线y=x2-2x+3与直线y=2x相交于A、B,抛物线与y轴相交于C点,求:△ABC的面积.
分析 首先两个函数联立方程组求得A、B两点的坐标,利用二次函数与y轴的交点坐标求得点C的坐标,利用△ABC的面积=△QBC的面积-△AOC的面积计算得出答案即可.
解答 解:∵抛物线y=x2-2x+3与直线y=2x相交于A、B,
∴$\left\{\begin{array}{l}{y={x}^{2}-2x+3}\\{y=2x}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=3}\\{y=6}\end{array}\right.$,$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$,
∴A(1,2)、B(3,6),
∵抛物线与y轴相交于C点,
∴C(0,3),
∴S△ABC=S△QBC-S△AOC=$\frac{1}{2}$×3×3-$\frac{1}{2}$×3×1=3.
点评 此题考查一次函数与二次函数交点问题,以及三角形面积计算方法.

练习册系列答案
相关题目
11.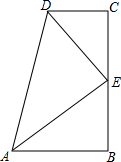 如图所示,在四边形ABCD中,∠B=∠C=90°,DE平分∠ADC,AE平分∠BAD,E在BC上,下列结论不成立的是( )
如图所示,在四边形ABCD中,∠B=∠C=90°,DE平分∠ADC,AE平分∠BAD,E在BC上,下列结论不成立的是( )
 如图所示,在四边形ABCD中,∠B=∠C=90°,DE平分∠ADC,AE平分∠BAD,E在BC上,下列结论不成立的是( )
如图所示,在四边形ABCD中,∠B=∠C=90°,DE平分∠ADC,AE平分∠BAD,E在BC上,下列结论不成立的是( )| A. | E是BC的中点 | B. | CD+AB=AD | C. | ∠AED=90° | D. | CE+DE=BC |
 如图.在△ABC中,BC=AC,CD是∠ACB的平分线.有下列结论:
如图.在△ABC中,BC=AC,CD是∠ACB的平分线.有下列结论: 如图所示,△ABC≌△DFE.试求∠FDB+∠ABD的值.
如图所示,△ABC≌△DFE.试求∠FDB+∠ABD的值. 如图,已知边长为2米的正方形铁架DEFG的正上方有一个灯泡A,测得铁架左右两边的影长分别为BE=6米,CF=4米,试求灯泡距地面的高度.
如图,已知边长为2米的正方形铁架DEFG的正上方有一个灯泡A,测得铁架左右两边的影长分别为BE=6米,CF=4米,试求灯泡距地面的高度.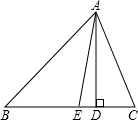 如图,在△ABC中,AD是边BC上的高,AE是∠A的角平分线,且∠C=60°,∠B=40°,求∠AED,∠EAD,∠CAD的度数.
如图,在△ABC中,AD是边BC上的高,AE是∠A的角平分线,且∠C=60°,∠B=40°,求∠AED,∠EAD,∠CAD的度数.