题目内容
3.若x2-$\sqrt{5}$x+1=0,则x4+x-4=7.分析 方程x2-$\sqrt{5}$x+1=0两边同时除以x解得:x-$\sqrt{5}$+$\frac{1}{x}$=0,即可求得x+$\frac{1}{x}$的值,然后两边平方即可求解x2+$\frac{1}{{x}^{2}}$的值,最后两边平方即可求解.
解答 解:方程x2-$\sqrt{5}$x+1=0两边同时除以x解得:x-$\sqrt{5}$+$\frac{1}{x}$=0,
则x+$\frac{1}{x}$=$\sqrt{5}$,
两边平方得:x2+2+$\frac{1}{{x}^{2}}$=5,则x2+$\frac{1}{{x}^{2}}$=3,
两边再平方得:x4+$\frac{1}{{x}^{4}}$+2=9,
则x4+$\frac{1}{{x}^{4}}$=7.
故答案为:7.
点评 本题考查了完全平方公式的应用以及代数式的求值,理解x+$\frac{1}{x}$与x2+$\frac{1}{{x}^{2}}$之间的关系是关键.

练习册系列答案
相关题目
11.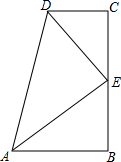 如图所示,在四边形ABCD中,∠B=∠C=90°,DE平分∠ADC,AE平分∠BAD,E在BC上,下列结论不成立的是( )
如图所示,在四边形ABCD中,∠B=∠C=90°,DE平分∠ADC,AE平分∠BAD,E在BC上,下列结论不成立的是( )
 如图所示,在四边形ABCD中,∠B=∠C=90°,DE平分∠ADC,AE平分∠BAD,E在BC上,下列结论不成立的是( )
如图所示,在四边形ABCD中,∠B=∠C=90°,DE平分∠ADC,AE平分∠BAD,E在BC上,下列结论不成立的是( )| A. | E是BC的中点 | B. | CD+AB=AD | C. | ∠AED=90° | D. | CE+DE=BC |
18.购一批水果,运输过程中损失10%,不计其他费用,要想获得至少20%的利润,则售价至少比进价提高 ( )
| A. | 34% | B. | 33.4% | C. | 33.3% | D. | 33% |
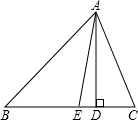 如图,在△ABC中,AD是边BC上的高,AE是∠A的角平分线,且∠C=60°,∠B=40°,求∠AED,∠EAD,∠CAD的度数.
如图,在△ABC中,AD是边BC上的高,AE是∠A的角平分线,且∠C=60°,∠B=40°,求∠AED,∠EAD,∠CAD的度数.