题目内容
4.(1)求不等式组$\left\{\begin{array}{l}{x-1≥1-x}\\{x+8>4x-1}\end{array}\right.$的整数解;(2)解方程:$\frac{x}{x-2}$-1=$\frac{1}{{x}^{2}-4}$.
分析 (1)先求出每个不等式的解集,再确定其公共解,得到不等式组的解集,然后求其整数解;
(2)求出这个分式方程即可.
解答 解:(1)解不等式①得:x≥1,
解不等式②得:x<3,
所以不等式组的解集是1≤x<3,
因为x取整数,
所以x=1,2
(2)原分式方程可化为:x(x+2)-(x-2)(x+2)=1,
解得:x=$-\frac{3}{2}$,
经检验x=$-\frac{3}{2}$是原方程的解.
点评 考查不等式组的解法及整数解的确定.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
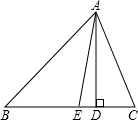 如图,在△ABC中,AD是边BC上的高,AE是∠A的角平分线,且∠C=60°,∠B=40°,求∠AED,∠EAD,∠CAD的度数.
如图,在△ABC中,AD是边BC上的高,AE是∠A的角平分线,且∠C=60°,∠B=40°,求∠AED,∠EAD,∠CAD的度数.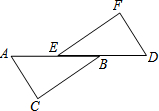 如图,A,E,B,D在同一直线上,在△ABC与△DEF中,AB=DE,AC=DF,AC∥DF.求证:∠C=∠F.
如图,A,E,B,D在同一直线上,在△ABC与△DEF中,AB=DE,AC=DF,AC∥DF.求证:∠C=∠F.