题目内容
13.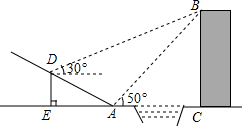 如图,贵阳市某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m.坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E,A,C在同一水平线上,求建筑物BC的高.(结果保留整数)
如图,贵阳市某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m.坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E,A,C在同一水平线上,求建筑物BC的高.(结果保留整数)
分析 过点D作DH⊥BC于点H,则四边形DHCE是矩形,DH=EC,DE=HC,设建筑物BC的高度为xm,则BH=(x-5)m,由三角函数得出DH=$\sqrt{3}$(x-5),AC=EC-EA=$\sqrt{3}$(x-5)-10,得出x=tan50°•[$\sqrt{3}$(x-5)],解方程即可.
解答 解:过点D作DH⊥BC于点M,如图所示:
则四边形DHCE是矩形,DH=EC,DE=HC,
设建筑物BC的高度为xm,则BH=(x-5)m,
在Rt△DHB中,∠BDH=30°,
∴DH=$\sqrt{3}$(x-5),AC=EC-EA=$\sqrt{3}$(x-5)-10,
在Rt△ACB中,∠BAC=50°,tan∠BAC=$\frac{BC}{AC}$,
∴x=tan50°•[$\sqrt{3}$(x-5)],
解得:x≈21,
答:建筑物BC的高约为21m.
点评 本题考查了仰角、坡角的定义,解直角三角形的应用,能借助仰角构造直角三角形,并结合图形利用三角函数解直角三角形是解题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
3.下列运算正确的是( )
| A. | 2a3•a4=a12 | B. | 2$\sqrt{2}$×$\sqrt{2}$=4 | C. | (2a4)3=8a7 | D. | a8÷a2=a4 |
5. 如图,在矩形ABCD中,点E,F分别是BC,DC上的一个动点,以EF为对称轴折叠△CEF,使点C的对称点G落在AD上,若AB=3,BC=5,则CF的取值范围为$\frac{5}{3}$≤CF≤3.
如图,在矩形ABCD中,点E,F分别是BC,DC上的一个动点,以EF为对称轴折叠△CEF,使点C的对称点G落在AD上,若AB=3,BC=5,则CF的取值范围为$\frac{5}{3}$≤CF≤3.
 如图,在矩形ABCD中,点E,F分别是BC,DC上的一个动点,以EF为对称轴折叠△CEF,使点C的对称点G落在AD上,若AB=3,BC=5,则CF的取值范围为$\frac{5}{3}$≤CF≤3.
如图,在矩形ABCD中,点E,F分别是BC,DC上的一个动点,以EF为对称轴折叠△CEF,使点C的对称点G落在AD上,若AB=3,BC=5,则CF的取值范围为$\frac{5}{3}$≤CF≤3.
2.下列说法正确的是( )
| A. | 在同一年出生的400人中至少有两人的生日相同 | |
| B. | 投掷一粒骰子,连投两次点数相同的概率与连投两次点数都为1的概率是相等的 | |
| C. | 从一副完整的扑克牌中随机抽取一张牌恰好是红桃K,这是必然事件 | |
| D. | 一个袋中装有3个红球,5个白球,任意摸出一个球是红球的概率是$\frac{3}{5}$ |
 折叠矩形ABCD,使点D落在BC边上的点F处,若折痕AE=5$\sqrt{5}$,tan∠EFC=$\frac{3}{4}$,则BC=10.
折叠矩形ABCD,使点D落在BC边上的点F处,若折痕AE=5$\sqrt{5}$,tan∠EFC=$\frac{3}{4}$,则BC=10. 如图,矩形ABCD中,AB=1,AD=2,点E是边AD上的一个动点,把△BAE沿BE折叠,点A落在A′处,如果A′恰在矩形的对称轴上,则AE的长为1或$\frac{\sqrt{3}}{3}$.
如图,矩形ABCD中,AB=1,AD=2,点E是边AD上的一个动点,把△BAE沿BE折叠,点A落在A′处,如果A′恰在矩形的对称轴上,则AE的长为1或$\frac{\sqrt{3}}{3}$. 如图,用扳手拧螺母时,旋转中心为螺丝(母)的中心,旋转角为0°~360°的任意角(答案不唯一).
如图,用扳手拧螺母时,旋转中心为螺丝(母)的中心,旋转角为0°~360°的任意角(答案不唯一). 如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E
如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E