题目内容
18.一个不透明的口袋中共放有3个红球和11个黄球,这两种球除颜色外没有其他任何区别,若从口袋中随机取出一个球,则取到黄球的概率是$\frac{11}{14}$.分析 用黄球的个数除以球的总个数可得.
解答 解:∵不透明的袋中有除颜色外没有其他任何区别的3个红球和11个黄球,共14个球,其中黄球有11个,
∴从口袋中随机取出一个球,则取到黄球的概率是$\frac{11}{14}$,
故答案为:$\frac{11}{14}$.
点评 本题考查的是概率的求法.如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
相关题目
13.给出四个数:0,$\sqrt{3}$,$\frac{1}{2}$,1,其中最大的是( )
| A. | 0 | B. | $\sqrt{3}$ | C. | $\frac{1}{2}$ | D. | -1 |
3.下列运算正确的是( )
| A. | 2a3•a4=a12 | B. | 2$\sqrt{2}$×$\sqrt{2}$=4 | C. | (2a4)3=8a7 | D. | a8÷a2=a4 |
10. 现有一张圆心角为108°,半径为40cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为10cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的圆心角θ的大小是( )
现有一张圆心角为108°,半径为40cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为10cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的圆心角θ的大小是( )
 现有一张圆心角为108°,半径为40cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为10cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的圆心角θ的大小是( )
现有一张圆心角为108°,半径为40cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为10cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的圆心角θ的大小是( )| A. | 18° | B. | 36° | C. | 72° | D. | 90° |
7.正六边形的边心距是$\sqrt{3}$,则它的边长是( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\frac{2}{3}$$\sqrt{3}$ |
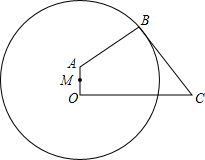 如图,为了保护运河入江口的古桥OA,规划建一座新桥BC,已知,古桥OA与河岸OC垂足,新桥BC与河岸AB垂直,且BC=AB,OC=210m,tan∠BCO=$\frac{4}{3}$.
如图,为了保护运河入江口的古桥OA,规划建一座新桥BC,已知,古桥OA与河岸OC垂足,新桥BC与河岸AB垂直,且BC=AB,OC=210m,tan∠BCO=$\frac{4}{3}$. 如图,矩形ABCD中,AB=1,AD=2,点E是边AD上的一个动点,把△BAE沿BE折叠,点A落在A′处,如果A′恰在矩形的对称轴上,则AE的长为1或$\frac{\sqrt{3}}{3}$.
如图,矩形ABCD中,AB=1,AD=2,点E是边AD上的一个动点,把△BAE沿BE折叠,点A落在A′处,如果A′恰在矩形的对称轴上,则AE的长为1或$\frac{\sqrt{3}}{3}$.