题目内容
3.分解因式:(1)a2-$\frac{4}{9}$b2
(2)9-4(x+y)2
(3)x2y-y
(4)-a4+1.
分析 (1)直接利用平方差公式分解因式得出答案;
(2)直接利用平方差公式分解因式得出答案;
(3)直接提取公因式y,进而利用平方差公式分解因式即可;
(4)直接利用平方差公式分解因式得出答案.
解答 解:(1)a2-$\frac{4}{9}$b2=(a+$\frac{2}{3}$b)(a-$\frac{2}{3}$b);
(2)9-4(x+y)2
=[3-2(x+y)][3+2(x+y)]
=(3-2x-2y)(3+2x+2y);
(3)x2y-y=y(x2-1)
=y(x+1)(x-1);
(4)-a4+1=(1+a2)(1-a2)=(1+a2)(1+a)(1-a).
点评 此题主要考查了提取公因式法以及公式法分解因式,正确应用平方差公式是解题关键.

练习册系列答案
相关题目
14.一手机经销商计划购进某品牌的A型、B型、C型三款手机共60部,设购进A型手机x部,B型手机y部,三款手机的进价和预售价如表:
(1)请用含x、y的代数式表示购买手机的预售总额,并进行化简;
(2)假设所购进手机恰好用去61000元且全部售出,综合考虑各种因素,该手机经销商在购销这批手机过程中需另外支出各种费用共1500元.请用含x的代数式表示预估利润,并进行化简(注:预估利润P=预售总额-购机款-各种费用).
| 手机型号 | A型 | B型 | C型 |
| 进价(单位:元/部) | 900 | 1200 | 1100 |
| 预售价(单位:元/部) | 1200 | 1600 | 1300 |
(2)假设所购进手机恰好用去61000元且全部售出,综合考虑各种因素,该手机经销商在购销这批手机过程中需另外支出各种费用共1500元.请用含x的代数式表示预估利润,并进行化简(注:预估利润P=预售总额-购机款-各种费用).
2. 如图,在△ABC、△ADE中,C、D两点分别在AE、AB上,BC、DE交于点F,若BD=DC=CE,∠ADC+∠ACD=114°,则∠DFC为( )
如图,在△ABC、△ADE中,C、D两点分别在AE、AB上,BC、DE交于点F,若BD=DC=CE,∠ADC+∠ACD=114°,则∠DFC为( )
 如图,在△ABC、△ADE中,C、D两点分别在AE、AB上,BC、DE交于点F,若BD=DC=CE,∠ADC+∠ACD=114°,则∠DFC为( )
如图,在△ABC、△ADE中,C、D两点分别在AE、AB上,BC、DE交于点F,若BD=DC=CE,∠ADC+∠ACD=114°,则∠DFC为( )| A. | 114° | B. | 123° | C. | 132° | D. | 147° |
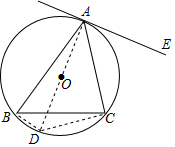 如图,已知△ABC内接于⊙O,AE为⊙O的切线,求证:∠CAE=∠ABC.
如图,已知△ABC内接于⊙O,AE为⊙O的切线,求证:∠CAE=∠ABC. 如图,正方形OABC和正方形DEFG是位似图形,点B坐标为(-1,1),点F坐标为(4,2),且位似中心在这两个图形的同侧,则位似中心的坐标为(-4,0).
如图,正方形OABC和正方形DEFG是位似图形,点B坐标为(-1,1),点F坐标为(4,2),且位似中心在这两个图形的同侧,则位似中心的坐标为(-4,0).