题目内容
7. 如图,在△ABC中,∠ACB=70°,∠1=∠2,则∠BPC的度数为( )
如图,在△ABC中,∠ACB=70°,∠1=∠2,则∠BPC的度数为( )| A. | 110° | B. | 70° | C. | 130° | D. | 不能确定 |
分析 先根据∠1=∠2得出∠2+∠BCP=∠ACB,再由三角形内角和定理即可得出结论.
解答 解:∵在△ABC中,∠ACB=70°,∠1=∠2,
∴∠2+∠BCP=∠ACB=70°,
∴∠BPC=180°-70°=110°.
故选A.
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
2. 如图,在△ABC、△ADE中,C、D两点分别在AE、AB上,BC、DE交于点F,若BD=DC=CE,∠ADC+∠ACD=114°,则∠DFC为( )
如图,在△ABC、△ADE中,C、D两点分别在AE、AB上,BC、DE交于点F,若BD=DC=CE,∠ADC+∠ACD=114°,则∠DFC为( )
 如图,在△ABC、△ADE中,C、D两点分别在AE、AB上,BC、DE交于点F,若BD=DC=CE,∠ADC+∠ACD=114°,则∠DFC为( )
如图,在△ABC、△ADE中,C、D两点分别在AE、AB上,BC、DE交于点F,若BD=DC=CE,∠ADC+∠ACD=114°,则∠DFC为( )| A. | 114° | B. | 123° | C. | 132° | D. | 147° |
12.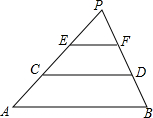 如图,已知AB∥CD∥EF,AC=CE=EP,△PEF的面积是2,则四边形ABCD的面积是( )
如图,已知AB∥CD∥EF,AC=CE=EP,△PEF的面积是2,则四边形ABCD的面积是( )
 如图,已知AB∥CD∥EF,AC=CE=EP,△PEF的面积是2,则四边形ABCD的面积是( )
如图,已知AB∥CD∥EF,AC=CE=EP,△PEF的面积是2,则四边形ABCD的面积是( )| A. | 18 | B. | 16 | C. | 12 | D. | 10 |
16.下列不一定是相似图形的是( )
| A. | 边数相同的正多边形 | B. | 两个等腰直角三角形 | ||
| C. | 两个圆 | D. | 两个等腰三角形 |
17.从多边形一条边上的一点(不是顶点)出发,连接各个顶点得到2013个三角形,则这个多边形的边数为( )
| A. | 2 011 | B. | 2 015 | C. | 2 014 | D. | 2 016 |
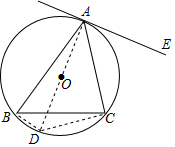 如图,已知△ABC内接于⊙O,AE为⊙O的切线,求证:∠CAE=∠ABC.
如图,已知△ABC内接于⊙O,AE为⊙O的切线,求证:∠CAE=∠ABC.