题目内容
4.下列算式结果为-2的是( )| A. | -|-2| | B. | (-2)0 | C. | -(-2) | D. | (-2)-1 |
分析 根据相反数的意义,非零的零次幂等于1,负整数指数幂与正整数指数幂互为倒数,可得答案.
解答 解:A、-|-2|=-2,故A正确;
B、(-2)0=1,故B错误;
C、-(-2)=2,故C错误;
D、(-2)-1=-$\frac{1}{2}$,故D错误;
故选:A.
点评 本题考查了负整数指数幂,利用负整数指数幂与正整数指数幂互为倒数是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.已知a-2b+3=0,则代数式5+2b-a的值是( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
9.(1)一个不透明的盒中装有若干个除颜色外都相同的红球与黄球.在这个口袋中先放入2个白球,再进行摸球试验,摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色后放回盒中,再继续摸球,全班一共做了400次这样的摸球试验.如果知道摸出白球的频数是40,你能估计在未放入白球前,袋中原来共有多少个小球吗?
(2)提出问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
活动操作:先从盒中摸出8个球,画上记号放回盒中.再进行摸球试验,摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色、是否有记号,放回盒中,再继续摸球、记录、放回袋中.
统计结果:摸球试验活动一共做了50次,统计结果如下表:
由上述的摸球试验推算:
①盒中红球、黄球各占总球数的百分比分别是多少?
②盒中有红球多少个?
(2)提出问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
活动操作:先从盒中摸出8个球,画上记号放回盒中.再进行摸球试验,摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色、是否有记号,放回盒中,再继续摸球、记录、放回袋中.
统计结果:摸球试验活动一共做了50次,统计结果如下表:
| 球的类别 | 无记号 | 有记号 | ||
| 红色 | 黄色 | 红色 | 黄色 | |
| 摸到的次数 | 18 | 28 | 2 | 2 |
①盒中红球、黄球各占总球数的百分比分别是多少?
②盒中有红球多少个?
13.下列图形不是轴对称图形的是( )
| A. | 正方形 | B. | 等腰三角形 | C. | 圆 | D. | 平行四边形 |
14.不等式2x+1>3的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
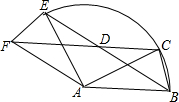 如图,△ABC中,AB=AC=2,∠BAC=30°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D,$\widehat{BE}$是点B旋转形成的弧.
如图,△ABC中,AB=AC=2,∠BAC=30°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D,$\widehat{BE}$是点B旋转形成的弧.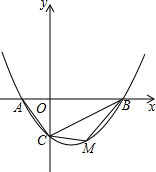 如图,抛物线y=ax2-$\frac{3}{2}$x-2(a≠0)的图象与x轴交于A,B两点,与y轴交于C点,已知B点坐标为(4,0).
如图,抛物线y=ax2-$\frac{3}{2}$x-2(a≠0)的图象与x轴交于A,B两点,与y轴交于C点,已知B点坐标为(4,0).