题目内容
4. 如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的角平分线.求证:DF∥AB
如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的角平分线.求证:DF∥AB证明:∵BE是∠ABC的角平分线
∴∠1=∠2(角平分线定义)
又∵∠E=∠1
∴∠E=∠2(等量代换)
∴AE∥BC(内错角相等,两直线平行)
∴∠A+∠ABC=180°(两直线平行,同旁内角互补)
又∵∠3+∠ABC=180°
∴∠A=∠3(同角的补角相等)
∴DF∥AB(同位角相等,两直线平行).
分析 根据角平分线定义求出∠1=∠2,求出∠E=∠2,根据平行线的判定得出AE∥BC,根据平行线的性质得出∠A+∠ABC=180°,求出∠A=∠3,根据平行线的判定得出即可.
解答 证明:BE是∠ABC的角平分线,
∴∠1=∠2(角平分线定义),
又∵∠E=∠1,
∴∠E=∠2(等量代换),
∴AE∥BC(内错角相等,两直线平行),
∴∠A+∠ABC=180°(两直线平行,同旁内角互补),
又∵∠3+∠ABC=180°,
∴∠A=∠3(同角的补角相等),
∴DF∥AB(同位角相等,两直线平行),
故答案为:(角平分线定义),(等量代换),(内错角相等,两直线平行),(两直线平行,同旁内角互补),(同角的补角相等),(同位角相等,两直线平行).
点评 本题考查了平行线的判定和性质的应用,能正确运用定理进行推理是解此题的关键,注意:平行线的判定有:①同位角相等,两直线平行,②内错角相等,两直线平行,③同旁内角互补,两直线平行,反之亦然.

练习册系列答案
相关题目
14.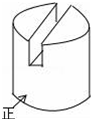 如图中几何体的左视图是( )
如图中几何体的左视图是( )
 如图中几何体的左视图是( )
如图中几何体的左视图是( )| A. | 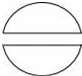 | B. |  | C. |  | D. | 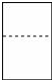 |
12.下列说法正确的个数有( )
①2是8的立方根; ②±4是64的立方根; ③无限小数都是无理数; ④带根号的数都是无理数.
①2是8的立方根; ②±4是64的立方根; ③无限小数都是无理数; ④带根号的数都是无理数.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
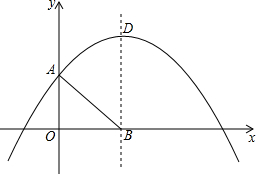 已知在直角坐标系中,抛物线y=ax2-8ax+3(a<0)与y轴交于点A,顶点为D,其对称轴交x轴于点B,点P在抛物线上,且位于抛物线对称轴的右侧.
已知在直角坐标系中,抛物线y=ax2-8ax+3(a<0)与y轴交于点A,顶点为D,其对称轴交x轴于点B,点P在抛物线上,且位于抛物线对称轴的右侧.