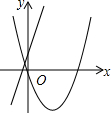��Ŀ����
20��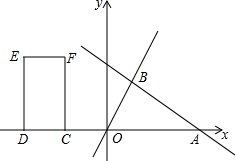 ��ͼ��ֱ��y=-$\frac{1}{2}$x+b��x���ڵ�A����ֱ��y=$\frac{3}{2}$x�ڵ�B��2��m��������CDEF�ı�DC��x���ϣ�D��C����࣬EF��x����Ϸ���DC=2��DE=4������C������Ϊ��-2��0��ʱ������CDEF��ʼ��ÿ��2����λ���ٶ���x�������˶����˶�ʱ��Ϊt�룮
��ͼ��ֱ��y=-$\frac{1}{2}$x+b��x���ڵ�A����ֱ��y=$\frac{3}{2}$x�ڵ�B��2��m��������CDEF�ı�DC��x���ϣ�D��C����࣬EF��x����Ϸ���DC=2��DE=4������C������Ϊ��-2��0��ʱ������CDEF��ʼ��ÿ��2����λ���ٶ���x�������˶����˶�ʱ��Ϊt�룮��1����b��m��ֵ��
��2������CDEF�˶�t��ʱ��ֱ��д��C��D��������꣨�ú�t�Ĵ���ʽ��ʾ����
��3������B�ھ���CDEF��һ����ʱ����t��ֵ��
���� ��1����B��2��m������y=$\frac{3}{2}x$�������m��ֵ��Ȼ�����y=-$\frac{1}{2}$x+b�������b��ֵ��
��2������C�������CD�ij������D�����꣬���˶�ʱ��λt���������˶�������2t����C��D��������꼴����⣻
��3����B�ھ���CDEF��һ���ϣ��������CF�ϻ�DE�ϣ���CF��ʱ��B�ĺ��������C�ĺ����꣬�����з�����⣬ͬ����B��DE��ʱ��B�ĺ��������D�ĺ����꣬�������t��
��� �⣺��1����B��2��m������y=$\frac{3}{2}x$�ã�m=$\frac{3}{2}��2$=3��
��B�������ǣ�2��3��������y=-$\frac{1}{2}$x+b�ã�-1+b=3����ã�b=4��
��2����DC=2����C������Ϊ��-2��0������D�������ǣ�-4��0����
�����CDEF�˶�t��ʱ��C�������ǣ�-2+2t��0����D������꣨-4+2t��0����
��3����B��CF��ʱ��-2+2t=2�����t=2��
��B��DE��ʱ��-4+2t=2�����t=3��
��t��ֵ��2��3��
���� ���⿼����һ�κ�����ͼ�ε�ƽ�ƣ���ȷ����B��CF��ʱ��B�ĺ��������C�ĺ����꣬ת��Ϊ��������ǹؼ���

��ϰ��ϵ�д�
 �����Ƹ���ʦ����ϵ�д�
�����Ƹ���ʦ����ϵ�д� ��ͨ����ͬ����ϰ��ϵ�д�
��ͨ����ͬ����ϰ��ϵ�д� ����С����ͬ������ϵ�д�
����С����ͬ������ϵ�д�
�����Ŀ
8��ֱ��y=kx+b-1�������ڶ����ޣ���k��b������ǣ�������
| A�� | k��0��b��1 | B�� | k��0��b��1 | C�� | k��0��b��1 | D�� | k��0��b��1 |
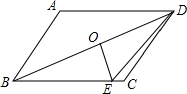 ��ͼ����?ABCD�У�O�ǶԽ���BD���е㣬��AB��AD������O��OE��BD�ڵ�E����?ABCD���ܳ�Ϊ20�����CDE���ܳ�Ϊ10��
��ͼ����?ABCD�У�O�ǶԽ���BD���е㣬��AB��AD������O��OE��BD�ڵ�E����?ABCD���ܳ�Ϊ20�����CDE���ܳ�Ϊ10��