题目内容
9.在同一平面直角坐标系中,函数y=ax2+bx与y=bx+a的图象可能是( )| A. | 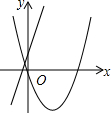 | B. | 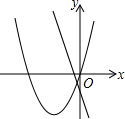 | C. | 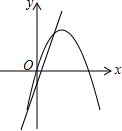 | D. | 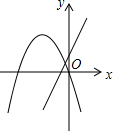 |
分析 首先根据图形中给出的一次函数图象确定a、b的符号,进而运用二次函数的性质判断图形中给出的二次函数的图象是否符合题意,根据选项逐一讨论解析,即可解决问题.
解答 解:A、对于直线y=bx+a来说,由图象可以判断,a>0,b>0;而对于抛物线y=ax2+bx来说,对称轴x=-$\frac{b}{2a}$<0,应在y轴的左侧,故不合题意,图形错误.
B、对于直线y=bx+a来说,由图象可以判断,a<0,b<0;而对于抛物线y=ax2+bx来说,图象应开口向下,故不合题意,图形错误.
C、对于直线y=bx+a来说,由图象可以判断,a<0,b>0;而对于抛物线y=ax2+bx来说,图象开口向下,对称轴x=-$\frac{b}{2a}$位于y轴的右侧,故符合题意,
D、对于直线y=bx+a来说,由图象可以判断,a>0,b>0;而对于抛物线y=ax2+bx来说,图象开口向下,a<0,故不合题意,图形错误.
故选:C.
点评 此主要考查了一次函数、二次函数图象的性质及其应用问题;解题的方法是首先根据其中一次函数图象确定a、b的符号,进而判断另一个函数的图象是否符合题意;解题的关键是灵活运用一次函数、二次函数图象的性质来分析、判断、解答.

练习册系列答案
相关题目
1.若抛物线y=x2-2x+c与x轴的一个交点为(3,0),则下列说法不正确的是( )
| A. | 抛物线开口向上 | |
| B. | 抛物线的对称轴是x=1 | |
| C. | 当x=1时,y的最大值为-4 | |
| D. | 关于x的一元二次方程x2-2x+c的两个根为-1,3 |
19.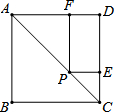 如图,在正方形ABCD中,对角线AC=6,点P是对角线AC上的一点,过点P作PF⊥AD,PE⊥CD,则PF+PE的值为( )
如图,在正方形ABCD中,对角线AC=6,点P是对角线AC上的一点,过点P作PF⊥AD,PE⊥CD,则PF+PE的值为( )
 如图,在正方形ABCD中,对角线AC=6,点P是对角线AC上的一点,过点P作PF⊥AD,PE⊥CD,则PF+PE的值为( )
如图,在正方形ABCD中,对角线AC=6,点P是对角线AC上的一点,过点P作PF⊥AD,PE⊥CD,则PF+PE的值为( )| A. | 3$\sqrt{2}$ | B. | 3 | C. | 2$\sqrt{3}$ | D. | 6 |
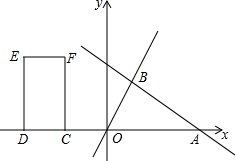 如图,直线y=-$\frac{1}{2}$x+b交x轴于点A,交直线y=$\frac{3}{2}$x于点B(2,m),矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴的上方,DC=2,DE=4.当点C的坐标为(-2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.
如图,直线y=-$\frac{1}{2}$x+b交x轴于点A,交直线y=$\frac{3}{2}$x于点B(2,m),矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴的上方,DC=2,DE=4.当点C的坐标为(-2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒. 如图,AD是△ABC的角平分线,∠B=30°,∠BAD=50°,求∠ADC和∠C的度数.
如图,AD是△ABC的角平分线,∠B=30°,∠BAD=50°,求∠ADC和∠C的度数.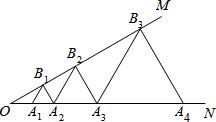 如图,已知,∠MON=30°,点A1,A2,A3在射线ON上,点B1,B2,B3…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形,若OA1=1,则△A4B4A5的边长为8.
如图,已知,∠MON=30°,点A1,A2,A3在射线ON上,点B1,B2,B3…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形,若OA1=1,则△A4B4A5的边长为8.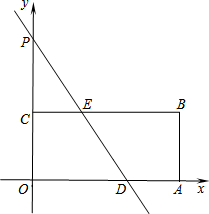 如图,在平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(12,0)、(12,6),直线y=kx+12与y轴交于点P,与边OA交于点D,与边BC交于点E.
如图,在平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(12,0)、(12,6),直线y=kx+12与y轴交于点P,与边OA交于点D,与边BC交于点E.