题目内容
 一个舞台要铺地毯(如图中的阴影部分,扇形的圆心角为90°),若按每铺1m2地毯所需30元计算,共需多少元(损耗不计)?
一个舞台要铺地毯(如图中的阴影部分,扇形的圆心角为90°),若按每铺1m2地毯所需30元计算,共需多少元(损耗不计)?考点:扇形面积的计算
专题:
分析:如图,求出扇形的半径,运用扇形的面积公式即可解决问题.
解答: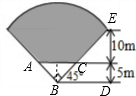 解:如图,△ABC、△BDE均为等腰直角三角形,
解:如图,△ABC、△BDE均为等腰直角三角形,
∵∠EBD=45°,∠EDB=90°,
∴∠BED=90°-45°=45°,
∴BD=ED=15;
由勾股定理得:BE2=BD2+DE2,
∴BE=15
;
同理可求:AB=CB=5
;
∴S阴影=
-
×5
×5
=
-25(m2).
∴铺设地板共需花费30×(
-25)=3375π-750(元).
 解:如图,△ABC、△BDE均为等腰直角三角形,
解:如图,△ABC、△BDE均为等腰直角三角形,∵∠EBD=45°,∠EDB=90°,
∴∠BED=90°-45°=45°,
∴BD=ED=15;
由勾股定理得:BE2=BD2+DE2,
∴BE=15
| 2 |
同理可求:AB=CB=5
| 2 |
∴S阴影=
90π•(15
| ||
| 360 |
| 1 |
| 2 |
| 2 |
| 2 |
=
| 225π |
| 2 |
∴铺设地板共需花费30×(
| 225π |
| 2 |
点评:该题主要考查了求阴影部分的面积问题;解题的关键是灵活运用扇形的面积公式来分析、判断、推理或解答.

练习册系列答案
相关题目
若2x-3=1,则3x+2的值是( )
| A、-1 | B、6 | C、8 | D、-8 |
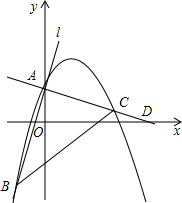 如图,抛物线y=ax2+bx+2与直线l交于点A、B两点,且A点为抛物线与y轴的交点,B(-2,-4),抛物线的对称轴是直线x=2,过点A作AC⊥AB,交抛物线于点C、x轴于点D.
如图,抛物线y=ax2+bx+2与直线l交于点A、B两点,且A点为抛物线与y轴的交点,B(-2,-4),抛物线的对称轴是直线x=2,过点A作AC⊥AB,交抛物线于点C、x轴于点D. “三月三,放风筝”,这天,妈妈让小玉自己动手制作一个如图所示的小风筝,它由两个三角形拼成,而且要满足△ABC≌△ADE才符合要求,小玉通过测量得到AB=AD,∠BAE=∠DAC,为了保证符合要求,还需要测量哪一对相等的量?请你帮助小玉找出一对相等的量并说明理由.
“三月三,放风筝”,这天,妈妈让小玉自己动手制作一个如图所示的小风筝,它由两个三角形拼成,而且要满足△ABC≌△ADE才符合要求,小玉通过测量得到AB=AD,∠BAE=∠DAC,为了保证符合要求,还需要测量哪一对相等的量?请你帮助小玉找出一对相等的量并说明理由. 如图,点O时直线AB上一点,∠AOD=120°,∠AOC=90°,OE平分∠BOD,则图中和为180°的两个角共有多少对?
如图,点O时直线AB上一点,∠AOD=120°,∠AOC=90°,OE平分∠BOD,则图中和为180°的两个角共有多少对?