题目内容
6.已知关于x的一元二次方程x2+2x-a=0的两个实根为x1,x2,且$\frac{1}{{x}_{1}}+\frac{1}{{x}_{2}}=\frac{2}{3}$,则a的值为3.分析 根据根与系数的关系得到x1+x2=-2,x1x2=a,代入$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{2}{3}$,然后解方程即可.
解答 解:∵关于x的一元二次方程x2+2x-a=0的两个实根为x1,x2,
∴x1+x2=-2,x1x2=-a,
∴$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{-2}{a}$=$\frac{2}{3}$,
∴a=3,
故答案为:3.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了一元二次方程的定义.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
17.已知a>b>c,设M=$\frac{2}{a-c}$,N=$\frac{1}{a-b}$+$\frac{1}{b-c}$.则M与N的大小关系为( )
| A. | M>N | B. | M=N | C. | M<N | D. | 无法确定 |
1.两个相似多边形的周长比是2:3,其中较小多边形的面积为4cm2,则较大多边形的面积为( )
| A. | 9cm2 | B. | 16cm2 | C. | 56cm2 | D. | 24cm2 |

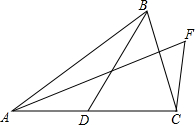 如图,AB=AC,∠ABD=∠CAF,∠F=∠BDC=60°.求证:BD+CF=AF.
如图,AB=AC,∠ABD=∠CAF,∠F=∠BDC=60°.求证:BD+CF=AF. 如图,已知点A在反比例函数y=$\frac{10}{x}$(x<0)的图象上,AD∥x轴,AB∥y轴,点B在反比例函数y=$\frac{k}{x}$(x<0)的图象上,过点B作BC∥x轴,交y轴于点C,若四边形ABCD的面积为8,则k的值为18.
如图,已知点A在反比例函数y=$\frac{10}{x}$(x<0)的图象上,AD∥x轴,AB∥y轴,点B在反比例函数y=$\frac{k}{x}$(x<0)的图象上,过点B作BC∥x轴,交y轴于点C,若四边形ABCD的面积为8,则k的值为18.