题目内容
8. 现有一面14米的长墙,某农户计划用32米长的篱笆靠墙围成一个矩形养鸡场ABCD(篱笆只围AB、BC、CD三边),其示意图如图所示.
现有一面14米的长墙,某农户计划用32米长的篱笆靠墙围成一个矩形养鸡场ABCD(篱笆只围AB、BC、CD三边),其示意图如图所示.(1)如果矩形养鸡场的面积为112平方米,求所用的墙长AD(结果精确到0.1米);
(2)求此矩形养鸡场的最大面积.
【参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73,$\sqrt{8}$=2.24】
分析 (1)直接表示出矩形的长与宽,进而得出等式求出答案;
(2)直接利用二次函数最值求法得出答案.
解答 解:(1)设AD=x,则BC=x,AB=$\frac{1}{2}$(32-x),根据题意可得:
x•$\frac{1}{2}$(32-x)=112,
解得:x1=16+4$\sqrt{2}$≈21.6(不合题意舍去),x2=16-4$\sqrt{2}$≈10.4,
答:所用的墙长AD约为10.4m;
(2)设矩形的面积为y,根据题意可得:
y=x•$\frac{1}{2}$(32-x)
=-$\frac{1}{2}$x2+16x
=-$\frac{1}{2}$(x-16)2+128,
答:此矩形养鸡场的最大面积为128m2.
点评 此题主要考查了一元二次方程的应用以及二次函数的应用,正确得出函数关系式是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.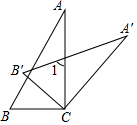 如图,把△ABC绕点C顺时针旋转某个角度θ得到△A′B′C,∠A=30°,∠1=70°,则旋转角θ可能等于( )
如图,把△ABC绕点C顺时针旋转某个角度θ得到△A′B′C,∠A=30°,∠1=70°,则旋转角θ可能等于( )
 如图,把△ABC绕点C顺时针旋转某个角度θ得到△A′B′C,∠A=30°,∠1=70°,则旋转角θ可能等于( )
如图,把△ABC绕点C顺时针旋转某个角度θ得到△A′B′C,∠A=30°,∠1=70°,则旋转角θ可能等于( )| A. | 40° | B. | 50° | C. | 70° | D. | 100° |
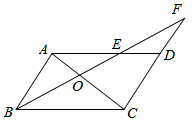 如图,在?ABCD中,过点B作直线交AC,AD于O,E,交CD的延长线于F.
如图,在?ABCD中,过点B作直线交AC,AD于O,E,交CD的延长线于F. 如图,△ABC是⊙O的内接正三角形,点M为$\widehat{BC}$上一动点,探索MA,MB,MC的关系.
如图,△ABC是⊙O的内接正三角形,点M为$\widehat{BC}$上一动点,探索MA,MB,MC的关系.