题目内容
19.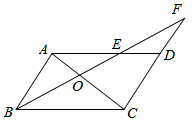 如图,在?ABCD中,过点B作直线交AC,AD于O,E,交CD的延长线于F.
如图,在?ABCD中,过点B作直线交AC,AD于O,E,交CD的延长线于F.(1)若OE=2,BE=5,求OA:OC的值;
(2)求证:OE:OB=OB:OF;
(3)若OE=2,OF=6,求OB的长.
分析 (1)先求出OB,再求出△AOE和△COB相似,根据相似三角形对应边成比例列式即可;
(2)求出△AOE和△COB相似,根据相似三角形对应边成比例可得OE:OB=OA:OC,再求出△AOB和△COF相似,根据相似三角形对应边成比例可得OA:OC=OB:OF,从而得证;
(3)将OE、OF的长代入(2)中计算即可得解.
解答 (1)解:∵OE=2,BE=5,
∴OB=BE-OE=5-2=3,
∵?ABCD中,AD∥BC,
∴△AOE∽△COB,
∴OA:OC=OE:OB=2:3;
(2)证明:∵?ABCD中,AD∥BC,
∴△AOE∽△COB,
∴OE:OB=OA:OC,
∵?ABCD中,AB∥CD,
∴△AOB∽△COF,
∴OA:OC=OB:OF,
∴OE:OB=OB:OF;
(3)解:∵OE:OB=OB:OF,
∴2:OB=OB:6,
解得OB=2$\sqrt{3}$.
点评 本题考查了相似三角形的判定与性质,平行四边形的性质,主要利用了相似三角形对应边成比例,难点在于(2)利用OA:OC作为中间比.

练习册系列答案
相关题目
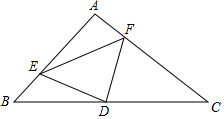 如图所示,在直角△ABC中,∠A=90°,AB=AC,点D为斜边BC上的中点,点E、F分别在直角边AB、AC上,且∠EDF=90°,求证:BE=AF.
如图所示,在直角△ABC中,∠A=90°,AB=AC,点D为斜边BC上的中点,点E、F分别在直角边AB、AC上,且∠EDF=90°,求证:BE=AF. 已知△ABC,利用三角板画平行线.
已知△ABC,利用三角板画平行线. 现有一面14米的长墙,某农户计划用32米长的篱笆靠墙围成一个矩形养鸡场ABCD(篱笆只围AB、BC、CD三边),其示意图如图所示.
现有一面14米的长墙,某农户计划用32米长的篱笆靠墙围成一个矩形养鸡场ABCD(篱笆只围AB、BC、CD三边),其示意图如图所示.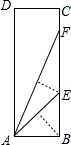 小明在学习“锐角三角函数”中发现,用折纸的方法可求出tan22.5°,方法如下:将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,这样就可以知道tan22.5°=$\sqrt{2}$-1.
小明在学习“锐角三角函数”中发现,用折纸的方法可求出tan22.5°,方法如下:将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,这样就可以知道tan22.5°=$\sqrt{2}$-1.