题目内容
11.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,若已知b=8及∠A=30°,则c的值为$\frac{16\sqrt{3}}{3}$.分析 根据∠C=90°,∠A=30°,于是得到c=2a,根据勾股定理得到c2-a2=b2,即:4a2-a2=64,求得a=$\frac{8\sqrt{3}}{3}$,结论得到结论.
解答 解:∵∠C=90°,∠A=30°,
∴c=2a,
∵b=8,
∴c2-a2=b2,
即:4a2-a2=64,
∴a=$\frac{8\sqrt{3}}{3}$,
∴c=$\frac{16\sqrt{3}}{3}$.
故答案为:$\frac{16\sqrt{3}}{3}$.
点评 本题考查了解直角三角形,直角三角形的性质,熟练掌握解直角三角形的方法是解题的关键.

练习册系列答案
相关题目
1.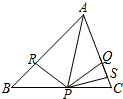 如图所示,已知△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则下列三个结论①AS=AR;②QP∥AR;③△BRP≌△CQP中( )
如图所示,已知△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则下列三个结论①AS=AR;②QP∥AR;③△BRP≌△CQP中( )
 如图所示,已知△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则下列三个结论①AS=AR;②QP∥AR;③△BRP≌△CQP中( )
如图所示,已知△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则下列三个结论①AS=AR;②QP∥AR;③△BRP≌△CQP中( )| A. | 全部正确 | B. | 仅①和②正确 | C. | 仅①正确 | D. | 仅①和③正确 |
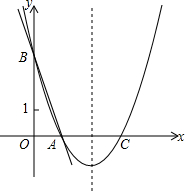 如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B.
如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B. 已知OC是∠AOB内部的一条射线,∠AOC=30°,OE是∠COB的平分线.当∠COE=40°时,求∠AOB的度数.
已知OC是∠AOB内部的一条射线,∠AOC=30°,OE是∠COB的平分线.当∠COE=40°时,求∠AOB的度数.