题目内容
1.若解分式方程$\frac{x-1}{x+4}=\frac{m}{x+4}$的解为正数,则m的取值范围是m>-1.分析 直接利用分式方程的解法表示出它的解,再利用它的解为正数,进而得出m的取值范围.
解答 解:$\frac{x-1}{x+4}=\frac{m}{x+4}$
去分母得:
x-1=m
解得:x=1+m,
∵分式方程$\frac{x-1}{x+4}=\frac{m}{x+4}$的解为正数,
∴1+m>0,
解得:m>-1.
故答案为:m>-1.
点评 此题主要考查了分式方程的解,正确掌握解分式方程的方法是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.若点A(a,b)在双曲线$y=\frac{3}{x}$上,则代数式ab-4的值为( )
| A. | -12 | B. | -7 | C. | -1 | D. | 1 |
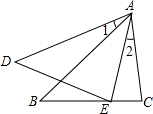 如图,已知∠1=∠2,∠AED=∠C,求证:△ABC∽△ADE.
如图,已知∠1=∠2,∠AED=∠C,求证:△ABC∽△ADE.