题目内容
1.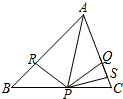 如图所示,已知△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则下列三个结论①AS=AR;②QP∥AR;③△BRP≌△CQP中( )
如图所示,已知△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则下列三个结论①AS=AR;②QP∥AR;③△BRP≌△CQP中( )| A. | 全部正确 | B. | 仅①和②正确 | C. | 仅①正确 | D. | 仅①和③正确 |
分析 根据角平分线性质求出∠PAB=∠PAC,∠PSA=∠PRA=90°,根据AAS推出△PAR≌△PAS,根据全等三角形的性质得出AR=AS,根据等腰三角形性质推出∠CAP=∠APQ,推出∠BAP=∠APQ,根据平行线的性质得出PQ∥AB,最后根据全等三角形的判定判断③即可.
解答 解:∵PR=PS,PR⊥AB于R,PS⊥AC于S,
∴∠PAB=∠PAC,∠PSA=∠PRA=90°,
在△PAR和△PAS中,
$\left\{\begin{array}{l}{∠PAR=∠PAS}\\{∠PRA=∠PSA}\\{AP=AP}\end{array}\right.$,
∴△PAR≌△PAS(AAS),
∴AR=AS,∴①正确;
∵AQ=PQ,
∠CAP=∠APQ,
∵∠CAP=∠BAP,
∴∠BAP=∠APQ,
∴PQ∥AB,∴②正确;
∵PR⊥AB,PS⊥AC,
∴∠PRB=∠PSC=90°,
∴PQ>PS,
∵PR=PS,
∴PQ>PR,
∴不能推出△BRP≌△CQP,∴③错误.
故选B.
点评 本题考查了全等三角形的性质和判定,角平分线性质,等腰三角形的性质的应用,能推出△PAR≌△PAS是解此题的关键.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
12.今年国庆长假期间,涪洋镇“家家福”超市某商品按标价打八折销售,小玲购了一件该商品,付款56元,则该项商品的标价为( )元.
| A. | 56 | B. | 68 | C. | 70 | D. | 72 |
16.给出四个数-2,0.5,$\frac{1}{3}$,$\sqrt{7}$,其中为无理数的是( )
| A. | -2 | B. | 0.5 | C. | $\frac{1}{3}$ | D. | $\sqrt{7}$ |
13.下列说法错误的是( )
| A. | 全等三角形是相似三角形 | |
| B. | 相似三角形周长的比等于对应边上高的比 | |
| C. | 在△ABC中,AD是BC边上的中线,G是重心,若GD=1,则AD=2 | |
| D. | 在△ABC中,D是AB的中点、E是AC的中点,若BC=10,则DE=5 |
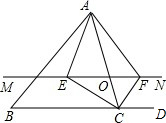 如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角∠ACD平分线于点F.
如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角∠ACD平分线于点F. 如图所示,在△ABC中,AC=9cm,DE垂直平分AB,如果△DBC的周长是16cm,那么BC的长度为7cm.
如图所示,在△ABC中,AC=9cm,DE垂直平分AB,如果△DBC的周长是16cm,那么BC的长度为7cm.