题目内容
2.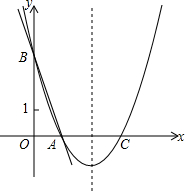 如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B.
如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B.(1)写出点A、B的坐标;
(2)求抛物线的函数表达式;
(3)在抛物线对称轴上存在一点P,使△ABP的周长最短.试求点P的坐标和该最短周长.
分析 (1)根据坐标轴上点的坐标特征求A,B两点的坐标;
(2)把A、B点坐标代入根据待定系数法求出a的值即可.
(3)先求得P的位置,然后求得直线BC的解析式,把x=2代入求得的解析式即可求得P点的坐标.
解答 解:(1)当y=0时,-3x+3=0,解得x=1,则A点坐标为(1,0);
当x=0时,y=-3x+3=3,则B点坐标为(0,3);
(2)∵抛物线过A(1,0)、B(0,3),
∴$\left\{\begin{array}{l}{a(1-2)^{2}+k=0}\\{a(0-2)^{2}+k=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=1}\\{k=-1}\end{array}\right.$,
∴抛物线解析式为y=(x-2)2-1.
(3)连接BC,交对称轴于P,此时PA+PB的值最小,即△ABP的周长最短,最短周长=AB+BC,
∵A点坐标为(1,0),对称轴为x=2,
∴C(3,0),
设直线BC的解析式为y=mx+n,
∵B(0,3),C(3,0),
∴$\left\{\begin{array}{l}{n=3}\\{3m+n=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-1}\\{n=3}\end{array}\right.$,
∴直线BC的解析式为y=-x+3,
令x=2,则y=-2+3=1,
∴P(2,1),
∵A(1,0),B(0,3),C(3,0);
∴AB=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,BC=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
∴最短周长为$\sqrt{10}$+3$\sqrt{2}$.
点评 本题考查了待定系数法求二次函数的解析式以及轴对称-最短路线问题,根据题意确定P的位置是解题的关键.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案| A. | -12 | B. | -7 | C. | -1 | D. | 1 |
(1)(-$\sqrt{5}$+$\sqrt{3}$)0=1
(2)[(x2)3]2=x8
(3)(a+b)(b+a)=a2+2ab+b2
(4)(-2a)3÷a=-8a2.
| A. | 1 | B. | 3 | C. | 2 | D. | 4 |
| A. | 56 | B. | 68 | C. | 70 | D. | 72 |
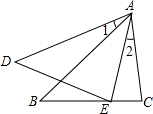 如图,已知∠1=∠2,∠AED=∠C,求证:△ABC∽△ADE.
如图,已知∠1=∠2,∠AED=∠C,求证:△ABC∽△ADE.