题目内容
6.某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.设该种品牌玩具的销售单价为x元(x>40),销售该品牌玩具获得利润w元,(1)请求出w与x的函数关系式.
(2)若商场要完成不少于480件的销售任务,且获得销售利润不少于10000元,求应将销售单价定为多少时才获得的最大利润?
分析 (1)由题意可得到w与x的函数关系式;
(2)由(1)中的函数关系式和题目中给出的信息可以求得应将销售单价定为多少时可获得最大利润.
解答 解:(1)由题意可得,
w=(x-30)[600-(x-40)×10]
化简,得w=-10x2+1300x-30000
即w与x的函数关系式是:w=-10x2+1300x-30000;
(2)由题意可得,
$\left\{\begin{array}{l}{600-(x-40)×10≥480}\\{-10{x}^{2}+1300x-30000≥10000}\end{array}\right.$
解不等式组,得50≤x≤52
∵w=-10x2+1300x-30000,在x<65时,w随x的增大而增大,
∴x=52时,获得最大利润,
即若商场要完成不少于480件的销售任务,且获得销售利润不少于10000元,应将销售单价定为52元时可获得最大利润.
点评 本题考查二次函数的应用,解题的关键是明确题意可以列出相应的函数关系式,由题目给出的信息可以求得函数的最值.

练习册系列答案
相关题目
16.给出四个数-2,0.5,$\frac{1}{3}$,$\sqrt{7}$,其中为无理数的是( )
| A. | -2 | B. | 0.5 | C. | $\frac{1}{3}$ | D. | $\sqrt{7}$ |
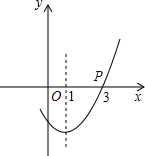 如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,且经过点P(4,0),则下列说法错误的有(1)(3).(1)c>0;(2)x=-2时y=0;(3)b2-4ac<0.
如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,且经过点P(4,0),则下列说法错误的有(1)(3).(1)c>0;(2)x=-2时y=0;(3)b2-4ac<0.