题目内容
7.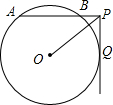 如图,⊙O中,点P是弦AB延长线上的一点,连接OP,过P作PQ⊥AP,且与⊙O相切于Q,若OP=4,∠APO=30°,则PA的长是( )
如图,⊙O中,点P是弦AB延长线上的一点,连接OP,过P作PQ⊥AP,且与⊙O相切于Q,若OP=4,∠APO=30°,则PA的长是( )| A. | 2$\sqrt{3}$+2$\sqrt{2}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{13}$ | D. | $\sqrt{13}$ |
分析 连接OQ,过O点作OC⊥AB与点C,由PQ⊥OQ,PQ⊥AP,OC⊥AB可得出四边形COQP为矩形,结合OP=4,∠APO=30°可算出OC和CP的长度,在Rt△ACO中,由OA与OC的长度结合勾股定理可得出AC的长度,AC+CP即可得出结论.
解答 解:连接OQ,过O点作OC⊥AB与点C,如图所示.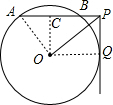
∵PQ与⊙O相切于Q,
∴PQ⊥OQ,
∵PQ⊥AP,OC⊥AB,
∴四边形COQP为矩形,
∵OP=4,∠APO=30°,
∴OC=2,CP=OQ=OA=2$\sqrt{3}$.
在Rt△ACO中,OC=2,OA=2$\sqrt{3}$,∠ACO=90°,
∴AC=$\sqrt{O{A}^{2}-O{C}^{2}}$=2$\sqrt{2}$,
∴AP=AC+CP=2$\sqrt{2}$+2$\sqrt{3}$.
故选A.
点评 本题考查了切线的性质、勾股定理以及解直角三角形,解题的关键是求出线段AC和线段CP的长度.本题属于基础题,难度不大,解决该类型题目时,根据切线的性质以及垂径定理得出线段间的关系是关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
17.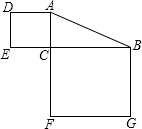 如图,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )
如图,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )
 如图,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )
如图,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )| A. | 150 | B. | 200 | C. | 225 | D. | 无法比较 |
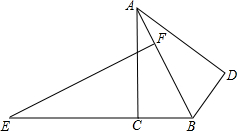 如图,直角三角形ABC中,∠ACB=90°,BC=3,AC=6,E为BC延长线上一点,且EC=$\frac{25}{4}$,过点E作EF⊥AB交AB于F,将△ABC沿AB翻折,得到△ABD,将△ABD绕点B旋转,在旋转过程中,记旋转中△ABD为△A′B′D′.设直线A′D′与射线EF交于点M,与射线EB交于点N,当△EMN是以∠MEN为底角的等腰三角形时,EN=13或$\frac{37}{4}$+3$\sqrt{5}$.
如图,直角三角形ABC中,∠ACB=90°,BC=3,AC=6,E为BC延长线上一点,且EC=$\frac{25}{4}$,过点E作EF⊥AB交AB于F,将△ABC沿AB翻折,得到△ABD,将△ABD绕点B旋转,在旋转过程中,记旋转中△ABD为△A′B′D′.设直线A′D′与射线EF交于点M,与射线EB交于点N,当△EMN是以∠MEN为底角的等腰三角形时,EN=13或$\frac{37}{4}$+3$\sqrt{5}$.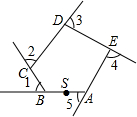 如图,五边形ABCDE是一块草地.小明从点S出发,沿着这个五边形的边步行一周,最后仍回到起点S处,小明在各拐弯处转过的角度之和是360°.
如图,五边形ABCDE是一块草地.小明从点S出发,沿着这个五边形的边步行一周,最后仍回到起点S处,小明在各拐弯处转过的角度之和是360°.