题目内容
11．
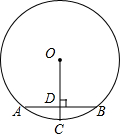如图，AB为⊙O的弦，AB=6cm，OC⊥AB于D，交⊙O于点C，且CD=1cm，则⊙O的半径为（ ）| A． | 5cm | B． | 6cm | C． | 8cm | D． | 10cm |
分析 根据垂径定理得到直角三角形，然后在直角三角形中运用勾股定理计算出半径的长．
解答 
解：如图：
连接OA，由OC⊥AB于D，得：AD=DB=$\frac{1}{2}$AB=3．
设⊙O的半径为r，
在Rt△OAD中，OA2=AD2+OD2
∴r2=（r-1）2+32
整理得：2r=10
∴r=5cm．
所以圆的半径是5cm．
故选A．
点评 本题考查的是垂径定理，根据垂径定理求出AD的长，连接OA，得到直角三角形，然后在直角三角形中计算出半径的长．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
1．已知点在线段上，下列条件中不能确定点C是线段AB中点的是（ ）
| A． | AC=BC | B． | AB=2AC | C． | AC+BC=AB | D． | $BC=\frac{1}{2}AB$ |
2．关于直线l：y=kx+k（k≠0），下列说法正确的是（ ）
| A． | l经过定点（1，0） | B． | l经过定点（-1，0） | ||
| C． | l经过第二、三、四象限 | D． | l经过第一、二、三象限 |
19．在平面直角坐标系中，抛物线y=-（x-1）2+2的顶点坐标是（ ）
| A． | （-1，2） | B． | （1，2） | C． | （2，-1） | D． | （2，1） |
6．
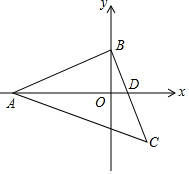如图，在等腰Rt△ABC中，∠ABC=90°，A（p，0），B（0，r），点C在第四象限，BC与x轴交于点D（q，0），x轴恰好平分∠BAC，则点C的坐标为（ ）
如图，在等腰Rt△ABC中，∠ABC=90°，A（p，0），B（0，r），点C在第四象限，BC与x轴交于点D（q，0），x轴恰好平分∠BAC，则点C的坐标为（ ）| A． | （r，$\frac{p-q}{2}$） | B． | （-$\frac{p}{2}$，$\frac{p-q}{2}$） | C． | （r，p+q） | D． | （2q，$\frac{p-r}{2}$） |
如图，锐角△ABC是⊙O内接三角形，弦AE⊥BC，垂足为D．在AD上取点F，使FD=DE，连接CF，并延长交AB于点G．求证：CG⊥AB．
如图，大正方形的边长为a，小正方形的边长为b．
9．为了鼓励市民节约用水，某市居民生活用水按阶梯式水价计费，如表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分信息：（水价计费=自来水销售费用+污水处理费用）
已知小王家2014年2月份用水20吨，交水费66元；3月份用水25吨，交水费91元．
（1）求a、b的值；
（2）随着夏天的到来用水量将增加，为了节约开支，小王计划把6月份水费控制在家庭月收入的2%，若小王家月收入为9200元，则小王家6月份最多能用水多少吨？
| 自来水销售价格 | 污水处理价格 | |
| 每户每月用水量 | 单价：元/吨 | 单价：元/吨 |
| 17吨及以下 | a | 0.80 |
| 超过17吨不超过30吨的部分 | b | 0.80 |
| 超过30吨的部分 | 6.00 | 0.80 |
（1）求a、b的值；
（2）随着夏天的到来用水量将增加，为了节约开支，小王计划把6月份水费控制在家庭月收入的2%，若小王家月收入为9200元，则小王家6月份最多能用水多少吨？