题目内容

1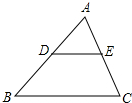．如图，在△ABC中，点D、E分别为AB、AC的中点，则△ADE与四边形BCED的面积比为（　　）
A．1：1B．1：2C．1：3D．1：4

分析 证明DE是△ABC的中位线，由三角形中位线定理得出DE∥BC，DE=$\frac{1}{2}$BC，证出△ADE∽△ABC，由相似三角形的性质得出△ADE的面积：△ABC的面积=1：4，即可得出结果．

解答 解：∵D、E分别为△ABC的边AB、AC上的中点，
∴DE是△ABC的中位线，
∴DE∥BC，DE=$\frac{1}{2}$BC，
∴△ADE∽△ABC，
∴△ADE的面积：△ABC的面积=（$\frac{1}{2}$）2=1：4，
∴△ADE的面积：四边形BCED的面积=1：3；
故选：C．

点评 本题考查了相似三角形的判定与性质、三角形中位线定理；熟记三角形中位线定理，证明三角形相似是解决问题的关键．

练习册系列答案
相关题目
11．在三角形的边上找出一点，使得该点与三角形的两顶点构成等腰三角形，这样的点有（　　）个．
A．4B．5C．6D．7
12．解下列方程：
（1）$\frac{x}{x-1}$-1=$\frac{4}{（x-1）（x+2）}$
（2）$\frac{1}{{x}^{3}+{2x}^{2}+x}$+$\frac{1}{{x}^{2}+2x+1}$=$\frac{5}{{2x}^{2}+2x}$．
9．如图，在三角形ABC中，∠BAC=130°，DE、FG分别垂直平分边AB和AC，那么∠DAF=80°．
16．下列各图中，∠1与∠2互为邻补角的是（　　）
A．B．C．D．
6．将一组数$\sqrt{2}$，2，$\sqrt{6}$，2$\sqrt{2}$，$\sqrt{10}$，…，2$\sqrt{10}$，按下列方式进行排列：
$\sqrt{2}$，2，$\sqrt{6}$，2$\sqrt{2}$，$\sqrt{10}$；
2$\sqrt{3}$，$\sqrt{14}$，4，3$\sqrt{2}$，2$\sqrt{5}$；
…
若2的位置记为（1，2），2$\sqrt{3}$的位置记为（2，1），则$\sqrt{38}$这个数的位置记为（　　）
A．（5，4）B．（4，4）C．（4，5）D．（3，5）
13．先化简，再求值：$\frac{{x}^{2}+2x+1}{{x}^{3}-x}$÷（1+$\frac{1}{x}$），其中x=$\sqrt{3}$+1．
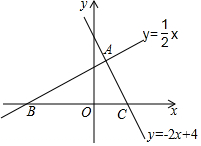11．已知直线y=-2x+4与y=$\frac{1}{2}$x+2，求它们与x轴围成的△ABC的面积．
12．先化简，再求值
（1）（5x-y）（y+2x）-（3y+2x）（3y-x），其中x=1，y=2
（2）（2a-3b）（-2a-3b）+（-2a+b）2，其中a=$\frac{1}{2}$，b=1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网