题目内容
9．
如图，在三角形ABC中，∠BAC=130°，DE、FG分别垂直平分边AB和AC，那么∠DAF=80°．
分析 先根据∠BAC=120°可得出∠B+∠C的度数，进而得出∠BAD+∠CAF的度数，故可得出结论．
解答 解：
∵∠BAC=130°，
∴∠B+∠C=180°-130°=50°．
∵DE、FG分别垂直平分AB和AC，
∴AD=BD，AF=CF，
∴∠BAD+∠CAF=∠B+∠C=50°，
∴∠DAF=130°-50°=80°．
故答案为：80．
点评 本题考查的是线段垂直平分线的性质，熟知线段垂直平分线上任意一点，到线段两端点的距离相等是解答此题的关键．
练习册系列答案
全能测控一本好卷系列答案
相关题目
19．将图1中的菱形剪开得到图2，则图2中共有4个菱形；将图2中的一个菱形剪开得到图3，则图3中共有7个菱形，…如此剪下去，请结合图形解决问题 
（1）按图示规律填写下表：
（2）按照这种方式剪下去，则第n个图中共有（3n-2）个菱形．
（3）按照这种方式剪下去，则第2017个图中共有6049个菱形．
（1）按图示规律填写下表：
| 图 | 1 | 2 | 3 | 4 | 5 | … |
| 菱形个数 | 1 | 4 | 7 | 10 | 13 | … |
（3）按照这种方式剪下去，则第2017个图中共有6049个菱形．
如图，AB是⊙O的直径，点C是半圆上的一个三等分点，点D是$\widehat{AC}$的中点，点P是直径AB上一点，若⊙O的半径为2，则PC+PD的最小值是2$\sqrt{2}$．
1．
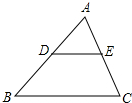如图，在△ABC中，点D、E分别为AB、AC的中点，则△ADE与四边形BCED的面积比为（ ）
如图，在△ABC中，点D、E分别为AB、AC的中点，则△ADE与四边形BCED的面积比为（ ）| A． | 1：1 | B． | 1：2 | C． | 1：3 | D． | 1：4 |
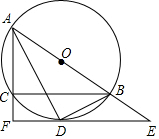如图，⊙O是△ABC的外接圆，AB为直径，∠BAC的平分线交⊙O于点D，过点D的切线分别交AB，AC的延长线于E，F，连接BD．
如图，EA∥BD，∠BAC=∠BCA，∠ACD=110°，求∠EAB的度数．