题目内容
15.如何把无限循环小数0.$\stackrel{.}{7}$3$\stackrel{.}{5}$,0.$\stackrel{.}{8}$23$\stackrel{.}{1}$化为分数形式?动手试一试,并总结循环小数化为分数形式的一般规律.分析 ①设0.$\stackrel{.}{7}$3$\stackrel{.}{5}$,=x,由0.$\stackrel{.}{7}$3$\stackrel{.}{5}$=0.735735…,得1000x=735.735735…,然后再列方程即可;
②方法与①类似,设0.$\stackrel{.}{8}$23$\stackrel{.}{1}$=y,有0.$\stackrel{.}{8}$23$\stackrel{.}{1}$=0.82318231…得10000x=8231.82318231…,然后再列方程即可.
解答 解:①设0.$\stackrel{.}{7}$3$\stackrel{.}{5}$,=x,由0.$\stackrel{.}{7}$3$\stackrel{.}{5}$=0.735735…,得1000x=735.735735….
可知,1000x-x=735,
解得:x=$\frac{245}{333}$,
②设0.$\stackrel{.}{8}$23$\stackrel{.}{1}$=y,有0.$\stackrel{.}{8}$23$\stackrel{.}{1}$=0.82318231…得10000x=8231.82318231…,
可得:10000x-x=8231,
解得:x=$\frac{8231}{9999}$.
点评 此题主要考查了一元一次方程的应用,解答本题的关键是找出其中的规律,即通过方程形式,把无限小数化成整数形式.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
3.一个多边形有两条对角线,则这个多边形是( )
| A. | 三角形 | B. | 四边形 | C. | 五边形 | D. | 六边形 |
5.若|a|=3,|b|=4,且|a-b|=b-a,则ab等于( )
| A. | 12 | B. | -12 | C. | 12或-12 | D. | 不能确定 |
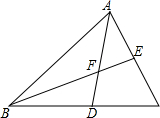 如图所示,△ABC的角平分线AD,BE相交于点F,∠C=60°,求证:AB=AE+BD.
如图所示,△ABC的角平分线AD,BE相交于点F,∠C=60°,求证:AB=AE+BD.