题目内容
7.已知△ABC中,AB=6,AC=BC=5,将△ABC折叠,使点A落在BC边上的点D处,折痕为EF(点E、F分别在边AB、AC上).(1)当ED⊥BC时,BE的长为$\frac{30}{9}$;
(2)当以B、E、D为顶点的三角形与△DEF相似时,BE的长为3或$\frac{14+16\sqrt{3}}{13}$.
分析 (1)如图1中,作CM⊥AB垂足为M,设AE=DE=x,由△EDB∽△CMB,得$\frac{EB}{BC}$=$\frac{DE}{CM}$,求出x即可解决问题.
(2)分两种情形如图2中,①当∠FED=∠EDB时,②当∠FED=∠DEB时,分别求解即可.
解答 解:(1)如图1中,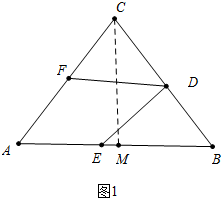 作CM⊥AB垂足为M,设AE=DE=x,
作CM⊥AB垂足为M,设AE=DE=x,
∵CA=CB=5,CM⊥AB,
∴AM=BM=3,∴CM=$\sqrt{B{C}^{2}-B{M}^{2}}$=4,
∵∠B=∠B,∠EDB=∠CMB=90°,
∴△EDB∽△CMB,
∴$\frac{EB}{BC}$=$\frac{DE}{CM}$,
∴$\frac{6-x}{5}$=$\frac{x}{4}$,
∴x=$\frac{24}{9}$,
∴BE=6-x=$\frac{30}{9}$.
故答案为$\frac{30}{9}$
(2)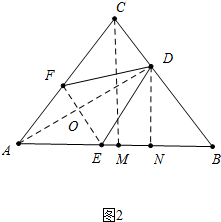 如图2中,①当∠FED=∠EDB时,∵∠B=∠EAF=∠EDF,∴△EDF∽△△DBE,
如图2中,①当∠FED=∠EDB时,∵∠B=∠EAF=∠EDF,∴△EDF∽△△DBE,
∴EF∥CB,设EF交AD于点O,
∵AO=OD,OE∥BD,
∴AE=EB=3,
②当∠FED=∠DEB时,则∠FED=∠FEA=∠DEB=60°,此时△FED∽△DEB,设AE=ED=x,作DN⊥AB于N,
则EN=$\frac{1}{2}$x,DN=$\frac{\sqrt{3}}{2}$x,∵DN∥CM,
∴$\frac{DN}{CM}$=$\frac{BN}{BM}$,
∴$\frac{\frac{\sqrt{3}}{2}x}{4}$=$\frac{6-\frac{3}{2}x}{3}$,
∴x=$\frac{16(4-\sqrt{3})}{13}$,
∴BE=6-x=$\frac{14+16\sqrt{3}}{13}$,
∴BE=3或$\frac{14+16\sqrt{3}}{13}$,
故答案为3或$\frac{14+16\sqrt{3}}{13}$.
点评 本题考查了相似三角形的判定与性质:有两个角对应相等的两个三角形相似;相似三角形的对应边的比相等.也考查了折叠的性质以及等腰三角形的性质,学会分类讨论的思想,不能漏解,属于中考常考题型.

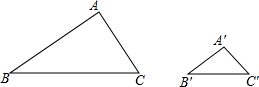 已知△ABC∽△A′B′C′,$\frac{AB}{A′B′}$=$\frac{BC}{B′C′}$=$\frac{CA}{C′A′}$=k,求证:$\frac{{C}_{△ABC}}{C△A′B′C′}$=k.
已知△ABC∽△A′B′C′,$\frac{AB}{A′B′}$=$\frac{BC}{B′C′}$=$\frac{CA}{C′A′}$=k,求证:$\frac{{C}_{△ABC}}{C△A′B′C′}$=k.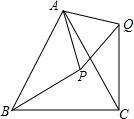 如图,等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ.
如图,等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ.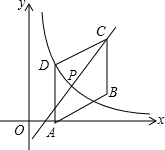 如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3).反比例函数y=$\frac{m}{x}$(x>0)的图象经过点D.(1,2)
如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3).反比例函数y=$\frac{m}{x}$(x>0)的图象经过点D.(1,2)