题目内容
16. 如图,在△ABC中,AB=5,BC=3,CA=4,AD平分∠BAC,点M,N分别为AD,AC上的动点,则CM+MN的最小值是2.4.
如图,在△ABC中,AB=5,BC=3,CA=4,AD平分∠BAC,点M,N分别为AD,AC上的动点,则CM+MN的最小值是2.4.
分析 取点N关于AD的对称点E,由轴对称图形的性质可知MN=ME,从而得到CM+MN=CM+ME,当点C、M、E在一条直线上且CE⊥AB时,CM+MN有最小值,然后证明△ABC为直角三角形,最后利用面积法求得CE的值即可.
解答 解:取点N关于AD的对称点E.
∵AD平分∠BAC,
∴点E在AB上.
∵点N与点D关于AD对称,
∴MN=ME.
∴CM+MN=CM+ME.
当CE⊥AB时,CE有最小值,即CM+MN有最小值.
在△ABC中,AB=5,BC=3,CA=4,
∴△ABC为直角三角形.
∴AC•BC=AB•CE,即5CE=3×4,解得CE=2.4.
故答案为:2.4.
点评 本题主要考查的是轴对称-路径最短问题,解答本题主要应用了轴对称图形的性质、垂线段最短的性质,将CM+MN转化为CE的长是解题的关键.

练习册系列答案
相关题目
7. 如图,在?ABCD中,下列结论错误的是( )
如图,在?ABCD中,下列结论错误的是( )
 如图,在?ABCD中,下列结论错误的是( )
如图,在?ABCD中,下列结论错误的是( )| A. | ∠1=∠2 | B. | ∠1=∠3 | C. | AB=CD | D. | ∠BAD=∠BCD |
11.如图,小明使一长为8厘米,宽为6厘米的长方形木板在桌面上作无滑动的滚动(顺时针方向),木板上的点A位置变化为A→A1→A2,其中第二次翻滚时被桌面上一小木块挡住,使木块与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( )


| A. | 20厘米 | B. | 8π厘米 | C. | 7π厘米 | D. | 5π厘米 |
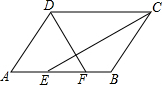 如图,在?ABCD中,∠ADC、∠DCB的平分线分别交边AB于点F,E.
如图,在?ABCD中,∠ADC、∠DCB的平分线分别交边AB于点F,E.
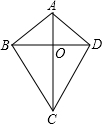 如图,四边形ABCD的对角线AC、BD相交于点O,△ABO≌△ADO,下列结论:①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.其中所有正确结论的个数有( )
如图,四边形ABCD的对角线AC、BD相交于点O,△ABO≌△ADO,下列结论:①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.其中所有正确结论的个数有( )