题目内容
17.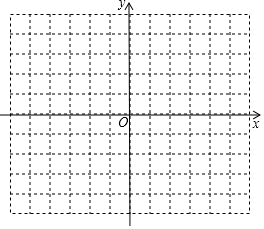 如图,在平面直角坐标系中,图中小正方形的边长均为1,已知△ABC三个顶点的坐标分别为A(-2,2),B(-4,0),C(-4,-4).
如图,在平面直角坐标系中,图中小正方形的边长均为1,已知△ABC三个顶点的坐标分别为A(-2,2),B(-4,0),C(-4,-4).(1)画出△ABC,以原点O为位似中心,将△ABC缩小为原来的$\frac{1}{2}$,得到△A1B1C1;
(2)求∠A1C1B1的正弦值.
分析 (1)利用相似图形的性质结合相似比进而得出对应点位置,即可得出答案;
(2)利用勾股定理得出各边长,再利用锐角三角函数关系求出答案.
解答 解: (1)如图所示:△A1B1C1和△A2B2C2即为所求;
(1)如图所示:△A1B1C1和△A2B2C2即为所求;
(2)如图所示:∵A1C1=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∴sin∠A1C1B1=$\frac{1}{\sqrt{10}}$=$\frac{\sqrt{10}}{10}$.
点评 此题主要考查了位似变换以及锐角三角函数关系,正确得出对应点位置是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.某旅游团一行40人到一旅馆住宿,旅馆的客房有三人间、二人间、单人间三种,三人间每天178元/间,二人间每天128元/间,单人间每天98元/间.要把这40人安排好住宿,每天最少的住宿费用是( )
| A. | 2392元 | B. | 2394元 | C. | 2388元 | D. | 2412元 |
8.下列四组线段中,不构成比例线段的一组是( )
| A. | 2cm,3cm,4cm,6cm | B. | 1cm,$\sqrt{2}$cm,$\sqrt{3}cm$,$\sqrt{6}$cm | C. | 1cm,2cm,3cm,6cm | D. | 1cm,2cm,3cm,5cm |
12.某校九年级(2)班积极响应学校的号召,每位同学都向“希望工程”捐献图书,全班40名同学共捐图书320册.特别值得表扬的是李亮和王州两位同学,他们各捐献了50册图书.班长统计了全班捐书情况如表,被粗心的马小虎用墨水污染了一部分:
(1)分别求出该班级捐献7册图书和8册图书的人数.
(2)请算出捐书册数的平均数、中位数和众数,并判断其中哪些统计量不能反映该班同学捐书册数的一般状况,说明理由.
| 册数 | 4 | 5 | 6 | 7 | 8 | 50 |
| 人数 | 6 | 8 | 15 | 2 |
(2)请算出捐书册数的平均数、中位数和众数,并判断其中哪些统计量不能反映该班同学捐书册数的一般状况,说明理由.
2.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. | 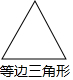 | B. | 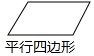 | C. |  | D. |  |
7. 如图,在?ABCD中,下列结论错误的是( )
如图,在?ABCD中,下列结论错误的是( )
 如图,在?ABCD中,下列结论错误的是( )
如图,在?ABCD中,下列结论错误的是( )| A. | ∠1=∠2 | B. | ∠1=∠3 | C. | AB=CD | D. | ∠BAD=∠BCD |
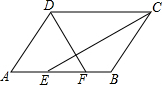 如图,在?ABCD中,∠ADC、∠DCB的平分线分别交边AB于点F,E.
如图,在?ABCD中,∠ADC、∠DCB的平分线分别交边AB于点F,E.