题目内容
16.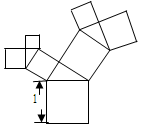 有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了该图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2016次后形成的图形中所有的正方形的面积和是( )
有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了该图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2016次后形成的图形中所有的正方形的面积和是( )| A. | 1 | B. | 2015 | C. | 2016 | D. | 2017 |
分析 求出每一次生长后所生长出的四边形面积,找出变化规律,计算出所有四边形的面积.
解答  解:如图,第一次生长后长出的三角形面积为SA+SB=1;
解:如图,第一次生长后长出的三角形面积为SA+SB=1;
第二次生长后长出的三角形面积为SD+SC+SA+SB=1;
第三次生长后长出的三角形面积为:1;
第四次生长后长出的三角形面积为:1;
…
“生长”了2016次后形成的图形中,所有的正方形的面积和是1×2016+1=2017.
故选D.
点评 此题考查了正方形的性质,以及勾股定理,其中能够根据勾股定理发现每一次得到的新的正方形的面积和与原正方形的面积之间的关系是解本题的关键.

练习册系列答案
相关题目
7.某旅游团一行40人到一旅馆住宿,旅馆的客房有三人间、二人间、单人间三种,三人间每天178元/间,二人间每天128元/间,单人间每天98元/间.要把这40人安排好住宿,每天最少的住宿费用是( )
| A. | 2392元 | B. | 2394元 | C. | 2388元 | D. | 2412元 |
1. 如图,已知D、E分别是△ABC的边AB、AC的中点,则S△ADE:S四边形DECB=( )
如图,已知D、E分别是△ABC的边AB、AC的中点,则S△ADE:S四边形DECB=( )
 如图,已知D、E分别是△ABC的边AB、AC的中点,则S△ADE:S四边形DECB=( )
如图,已知D、E分别是△ABC的边AB、AC的中点,则S△ADE:S四边形DECB=( )| A. | 1:2 | B. | 1:3 | C. | 2:3 | D. | 1:4 |
8.下列四组线段中,不构成比例线段的一组是( )
| A. | 2cm,3cm,4cm,6cm | B. | 1cm,$\sqrt{2}$cm,$\sqrt{3}cm$,$\sqrt{6}$cm | C. | 1cm,2cm,3cm,6cm | D. | 1cm,2cm,3cm,5cm |
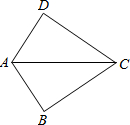 如图,四边形ABCD中,BC=DC,要使△ABC≌△ADC,还需要添加一个条件,你添加的条件是AD=AB或者∠ACD=∠ACB或者∠B=∠D=90°(写一个即可).
如图,四边形ABCD中,BC=DC,要使△ABC≌△ADC,还需要添加一个条件,你添加的条件是AD=AB或者∠ACD=∠ACB或者∠B=∠D=90°(写一个即可).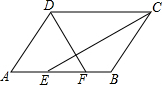 如图,在?ABCD中,∠ADC、∠DCB的平分线分别交边AB于点F,E.
如图,在?ABCD中,∠ADC、∠DCB的平分线分别交边AB于点F,E.