题目内容
7.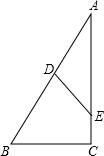 如图,∠A+∠B=90°,点D在线段AB上,点E在线段AC上.
如图,∠A+∠B=90°,点D在线段AB上,点E在线段AC上.(1)作DF平分∠BDE,DF与BC交于点F.依题意用尺规补全图形;
(2)若∠B+∠BDF=90°,求证:AD=DE
证明:∵∠A+∠B=90°,∠B+∠BDF=90°(已知)
∴∠A=∠BDF(理由:同角的余角相等或等式性质).
∴AC∥DF(理由:同位角相等,两直线平行).
∴∠AED=∠EDF(理由:两直线平行,内错角相等).
又∵∠BDF=∠EDF(已知)
∴∠A=∠AED(理由:等量代换).
∴AD=DE
(理由:等角对等边).
分析 (1)画出DF平分∠BDE;
(2)首先根据∠A+∠B=90°,∠B+∠BDF=90°可得∠A=∠BDF,再根据DF平分∠BDE可得∠BDF=∠EDF,进而可得∠A=∠EDF.
解答 (1)解:如图所示:
(2)证明:∵∠A+∠B=90°,∠B+∠BDF=90°(已知)
∴∠A=∠BDF(理由:同角的余角相等或等式性质).
∴AC∥DF(理由:同位角相等,两直线平行).
∴∠AED=∠EDF(理由:两直线平行,内错角相等).
又∵∠BDF=∠EDF(已知)
∴∠A=∠AED(理由:等量代换).
∴AD=DE(理由:等角对等边).
故答案为:∠A=∠BDF,(同角的余角相等或等式性质),
同位角相等,两直线平行.
两直线平行,内错角相等.
等量代换,等角对等边.
点评 此题主要考查了角平分线的性质,以及余角的性质,关键是掌握等角的补角相等.等角的余角相等.

练习册系列答案
相关题目
20.若-$\frac{a}{3}$≤-$\frac{a}{2}$,则a一定满足( )
| A. | a>0 | B. | a<0 | C. | a≥0 | D. | a≤0 |
12.已知实数a,b分别满足a2-6a+4=0,b2-6b+4=0,且a≠b,则a2+b2的值为( )
| A. | 36 | B. | 50 | C. | 28 | D. | 25 |
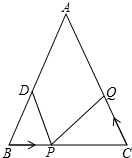 如图,AB=AC=10cm,BC=8cm,点D为AB的中点,点P在线段BC上以3cm/秒的速度由点B向点C运动,同时,点Q在线段CA上由C点向A点运动.
如图,AB=AC=10cm,BC=8cm,点D为AB的中点,点P在线段BC上以3cm/秒的速度由点B向点C运动,同时,点Q在线段CA上由C点向A点运动.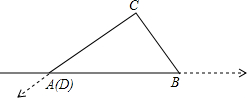 在数轴上点A、B、C、D分别对应数-3、7、13、21,把数轴两次弯折后使点D与点A重合,围成三角形ABC(如图所示),则sin∠ABC的值为$\frac{4}{5}$.
在数轴上点A、B、C、D分别对应数-3、7、13、21,把数轴两次弯折后使点D与点A重合,围成三角形ABC(如图所示),则sin∠ABC的值为$\frac{4}{5}$.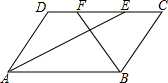 如图,在?ABCD中,AB=8cm,AD=5cm,∠BAD的平分线交CD于点E,∠ABC的平分线交CD于点F,则线段EF的长2cm.
如图,在?ABCD中,AB=8cm,AD=5cm,∠BAD的平分线交CD于点E,∠ABC的平分线交CD于点F,则线段EF的长2cm.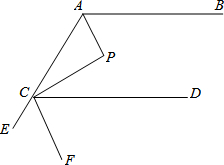 如图,AP,CP分别平分∠BAC,∠ACD,∠P=90°,设∠BAP=α.
如图,AP,CP分别平分∠BAC,∠ACD,∠P=90°,设∠BAP=α.