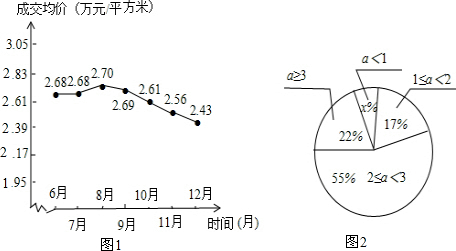
��Ŀ����
20��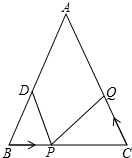 ��ͼ��AB=AC=10cm��BC=8cm����DΪAB���е㣬��P���߶�BC����3cm/����ٶ��ɵ�B���C�˶���ͬʱ����Q���߶�CA����C����A���˶���
��ͼ��AB=AC=10cm��BC=8cm����DΪAB���е㣬��P���߶�BC����3cm/����ٶ��ɵ�B���C�˶���ͬʱ����Q���߶�CA����C����A���˶�����1������Q���ٶ����P���ٶ���ȣ�1����ʱ����BPD���CQP�Ƿ�ȫ�ȣ���������Ͳ�˵����
��2����Q���ٶ����P���ٶȲ���ȣ�����Q���˶��ٶ�Ϊ����ʱ���ܹ�ʹ��BPD�ա�CPQ��
��3������Q�ԣ�2���е��ٶȴӵ�C��������P��ԭ���˶��ٶȴӵ�Bͬʱ����������ʱ����ABC�������˶������ʱ�䣬��P���Q��һ���ڡ�ABC������һ������������
���� ��1�����BP��CQ��CP������ȫ�������ε��ж��Ƴ����ɣ�
��2���赱��Q���˶��ٶ�Ϊxcm/�룬ʱ����t�룬�ܹ�ʹ��BPD���CQPȫ�ȣ����BD=5cm��BP=3tcm��CP=��8-3t��cm��CQ=xtcm����B=��C������ȫ�������ε����ʵó����̣�������̵Ľ⼴�ɣ�
��3����������ʱ��·�̲�Ϊ10+10���������ʱ��t��ֵ��
��� �⣺��1����Q���˶��ٶ����P���˶��ٶ���ȣ�����1���BPD���CQPȫ�ȣ�
�����ǣ���AB=AC=10cm����DΪAB���е㣬
���B=��C��BD=5cm��
��BP=CQ=3tcm=3cm��
��CP=8cm-3cm=5cm=BD��
�ڡ�DBP�͡�PCQ�У�
$\left\{\begin{array}{l}{BD=CP}\\{��B=��C}\\{BP=CQ}\end{array}\right.$��
���DBP�ա�PCQ��SAS����
��2���赱��Q���˶��ٶ�Ϊxcm/�룬ʱ����t�룬�ܹ�ʹ��BPD���CQPȫ�ȣ�
���BD=5cm��BP=3tcm��CP=��8-3t��cm��CQ=xtcm����B=��C��
�൱BP=CQ��BD=CP��BP=CP��BD=CQʱ����BPD���CQPȫ�ȣ�
����3t=xt��5=8-3t��
��ã�x=3���������⣬��ȥ����
��3t=8-3t��5=xt��
��ã�x=$\frac{15}{4}$��
������Q���˶��ٶ�Ϊ$\frac{15}{4}$cm/��ʱ���ܹ�ʹ��BPD���CQPȫ�ȣ�
��3���辭��x����P���Q��һ��������
�����⣬��$\frac{15}{4}$x=3x+2��10��
���x=$\frac{80}{3}$��
���P���˶���$\frac{80}{3}$��3=80cm��
��ABC�ܳ�Ϊ��10+10+8=28cm��
�����˶�����Ȧ��Ϊ��28��3=84cm��
��84-80=4cm��AB�ij��ȣ�
���P����Q��AB����������
�ྭ��$\frac{80}{3}$s��P���Q��һ���ڱ�AB��������
���� ���⿼����������ȫ�ȵ��ж������ʣ����������ε����ʣ��Լ����ν��˼������ã�����ĸ�������������������ȫ�ȵ��ж������ʣ�

 ����ͬ�����Ծ�ϵ�д�
����ͬ�����Ծ�ϵ�д�| A�� | 4 | B�� | 8 | C�� | 9 | D�� | 10 |
| A�� | x��1 | B�� | x��2 | C�� | x��1��x��2 | D�� | x��1��x��2 |
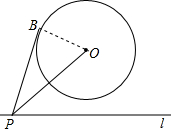 ��ͼ����O�İ뾶Ϊ2����O��ֱ��l�ľ���Ϊ3����P��ֱ��l�ϵ�һ�����㣮��PB�С�O�ڵ�B����PB����Сֵ�ǣ�������
��ͼ����O�İ뾶Ϊ2����O��ֱ��l�ľ���Ϊ3����P��ֱ��l�ϵ�һ�����㣮��PB�С�O�ڵ�B����PB����Сֵ�ǣ�������| A�� | $\sqrt{13}$ | B�� | $\sqrt{5}$ | C�� | 3 | D�� | 2 |
 ����ʱ��ʱ��Ӧ��12��01��
����ʱ��ʱ��Ӧ��12��01��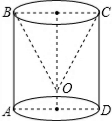 ��ͼ��Բ��������ȥһ���������ȸߵ�Բ����O��AD�ľ���Ϊ1����OCD=30�㣬OC=4������ȥԲ��ı�����ǣ�16+8$\sqrt{3}$���У�
��ͼ��Բ��������ȥһ���������ȸߵ�Բ����O��AD�ľ���Ϊ1����OCD=30�㣬OC=4������ȥԲ��ı�����ǣ�16+8$\sqrt{3}$���У�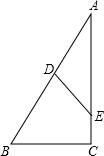 ��ͼ����A+��B=90�㣬��D���߶�AB�ϣ���E���߶�AC�ϣ�
��ͼ����A+��B=90�㣬��D���߶�AB�ϣ���E���߶�AC�ϣ�