题目内容
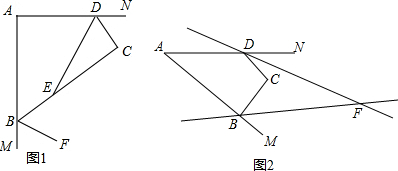
15.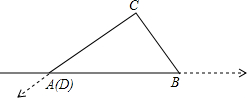 在数轴上点A、B、C、D分别对应数-3、7、13、21,把数轴两次弯折后使点D与点A重合,围成三角形ABC(如图所示),则sin∠ABC的值为$\frac{4}{5}$.
在数轴上点A、B、C、D分别对应数-3、7、13、21,把数轴两次弯折后使点D与点A重合,围成三角形ABC(如图所示),则sin∠ABC的值为$\frac{4}{5}$.
分析 根据题意求得AB=10,BC=6,AC=8,根据勾股定理的逆定理证得△ABC为直角三角形,∠C=90°,在RT△ABC中,根据正弦的定义即可求得.
解答 解:根据题意:AB=10,BC=6,AC=8,
∵BC2+AC2=36+64=100=102=AB2,
∴△ABC为直角三角形,∠C=90°,
∴sin∠ABC=$\frac{AC}{AB}$=$\frac{8}{10}$=$\frac{4}{5}$.
故答案为$\frac{4}{5}$.
点评 本题考查的是解直角三角形的应用,证得三角形ABC的直角三角形是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.已知一组数据10,8,9,x,4的众数是8,那么这组数据的中位数是( )
| A. | 4 | B. | 8 | C. | 9 | D. | 10 |
5.在函数中的y=$\frac{\sqrt{x-1}}{x-2}$,自变量x的取值范围是( )
| A. | x>1 | B. | x≠2 | C. | x>1且x≠2 | D. | x≥1且x≠2 |
11.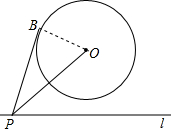 如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点.若PB切⊙O于点B,则PB的最小值是( )
如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点.若PB切⊙O于点B,则PB的最小值是( )
 如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点.若PB切⊙O于点B,则PB的最小值是( )
如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点.若PB切⊙O于点B,则PB的最小值是( )| A. | $\sqrt{13}$ | B. | $\sqrt{5}$ | C. | 3 | D. | 2 |
20.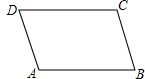 已知:如图,平行四边形ABCD,求作一个三角形,使三角形的面积等于平行四边形ABCD的面积.甲、乙两人的作法分别是:
已知:如图,平行四边形ABCD,求作一个三角形,使三角形的面积等于平行四边形ABCD的面积.甲、乙两人的作法分别是:
甲:
1.过C作AB的垂线段CE,垂足为E;
2.延长EC到点F,使得CE=CF;
3.连结AF、BF;△ABF即为所求的三角形
乙:
1.连结AC和BD,相交于点O;
2.延长OC到点E,使得OE=AC;
3.延长OB到点F,使得OF=DB;
4.连结EF;△OEF即为所求的三角形
对于甲、乙两人的作法,可判断( )
 已知:如图,平行四边形ABCD,求作一个三角形,使三角形的面积等于平行四边形ABCD的面积.甲、乙两人的作法分别是:
已知:如图,平行四边形ABCD,求作一个三角形,使三角形的面积等于平行四边形ABCD的面积.甲、乙两人的作法分别是:甲:
1.过C作AB的垂线段CE,垂足为E;
2.延长EC到点F,使得CE=CF;
3.连结AF、BF;△ABF即为所求的三角形
乙:
1.连结AC和BD,相交于点O;
2.延长OC到点E,使得OE=AC;
3.延长OB到点F,使得OF=DB;
4.连结EF;△OEF即为所求的三角形
对于甲、乙两人的作法,可判断( )
| A. | 甲、乙均正确 | B. | 甲、乙均错 | C. | 甲正确、乙错误 | D. | 甲错误,乙正确 |
4.下列说法正确的是( )
| A. | 对角线相等的四边形是平行四边形 | |
| B. | 对角线互相平分且相等的四边形是菱形 | |
| C. | 对角线互相垂直平分的四边形是矩形 | |
| D. | 对角线相等的菱形是正方形 |
 如图,点M在正方形ABCD的对角线BD上.求证:AM=CM.
如图,点M在正方形ABCD的对角线BD上.求证:AM=CM.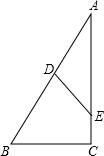 如图,∠A+∠B=90°,点D在线段AB上,点E在线段AC上.
如图,∠A+∠B=90°,点D在线段AB上,点E在线段AC上.