题目内容
12.已知实数a,b分别满足a2-6a+4=0,b2-6b+4=0,且a≠b,则a2+b2的值为( )| A. | 36 | B. | 50 | C. | 28 | D. | 25 |
分析 根据题意,a、b可看作方程x2-6x+4=0的两根,则根据根与系数的关系得到a+b=6,ab=4,然后把原式变形得到原式=再利用整体代入的方法计算即可.
解答 解:∵a2-6a+4=0,b2-6b+4=0,且a≠b,
∴a,b可看作方程x2-6x+4=0的两根,
∴a+b=6,ab=4,
∴原式=(a+b)2-2ab=62-2×4=28,
故选C.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
5.在函数中的y=$\frac{\sqrt{x-1}}{x-2}$,自变量x的取值范围是( )
| A. | x>1 | B. | x≠2 | C. | x>1且x≠2 | D. | x≥1且x≠2 |
20.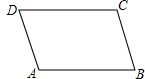 已知:如图,平行四边形ABCD,求作一个三角形,使三角形的面积等于平行四边形ABCD的面积.甲、乙两人的作法分别是:
已知:如图,平行四边形ABCD,求作一个三角形,使三角形的面积等于平行四边形ABCD的面积.甲、乙两人的作法分别是:
甲:
1.过C作AB的垂线段CE,垂足为E;
2.延长EC到点F,使得CE=CF;
3.连结AF、BF;△ABF即为所求的三角形
乙:
1.连结AC和BD,相交于点O;
2.延长OC到点E,使得OE=AC;
3.延长OB到点F,使得OF=DB;
4.连结EF;△OEF即为所求的三角形
对于甲、乙两人的作法,可判断( )
 已知:如图,平行四边形ABCD,求作一个三角形,使三角形的面积等于平行四边形ABCD的面积.甲、乙两人的作法分别是:
已知:如图,平行四边形ABCD,求作一个三角形,使三角形的面积等于平行四边形ABCD的面积.甲、乙两人的作法分别是:甲:
1.过C作AB的垂线段CE,垂足为E;
2.延长EC到点F,使得CE=CF;
3.连结AF、BF;△ABF即为所求的三角形
乙:
1.连结AC和BD,相交于点O;
2.延长OC到点E,使得OE=AC;
3.延长OB到点F,使得OF=DB;
4.连结EF;△OEF即为所求的三角形
对于甲、乙两人的作法,可判断( )
| A. | 甲、乙均正确 | B. | 甲、乙均错 | C. | 甲正确、乙错误 | D. | 甲错误,乙正确 |
17.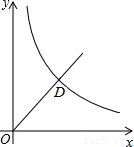 如图,在平面直角坐标系中,函数y=x和函数y=$\frac{16}{x}$的图象在第一象限交于点D(4,m),与平行于y轴的直线x=t(0<t<4)分别交于点A和点B,平面上有点P(0,6).若以点O,P,A,B为顶点的四边形为平行四边形,则这个平行四边形被直线PD所分割成的两部分图形的面积之比为( )
如图,在平面直角坐标系中,函数y=x和函数y=$\frac{16}{x}$的图象在第一象限交于点D(4,m),与平行于y轴的直线x=t(0<t<4)分别交于点A和点B,平面上有点P(0,6).若以点O,P,A,B为顶点的四边形为平行四边形,则这个平行四边形被直线PD所分割成的两部分图形的面积之比为( )
 如图,在平面直角坐标系中,函数y=x和函数y=$\frac{16}{x}$的图象在第一象限交于点D(4,m),与平行于y轴的直线x=t(0<t<4)分别交于点A和点B,平面上有点P(0,6).若以点O,P,A,B为顶点的四边形为平行四边形,则这个平行四边形被直线PD所分割成的两部分图形的面积之比为( )
如图,在平面直角坐标系中,函数y=x和函数y=$\frac{16}{x}$的图象在第一象限交于点D(4,m),与平行于y轴的直线x=t(0<t<4)分别交于点A和点B,平面上有点P(0,6).若以点O,P,A,B为顶点的四边形为平行四边形,则这个平行四边形被直线PD所分割成的两部分图形的面积之比为( )| A. | 1:1 | B. | 1:2 | C. | 1:3 | D. | 1:4 |
4.下列说法正确的是( )
| A. | 对角线相等的四边形是平行四边形 | |
| B. | 对角线互相平分且相等的四边形是菱形 | |
| C. | 对角线互相垂直平分的四边形是矩形 | |
| D. | 对角线相等的菱形是正方形 |
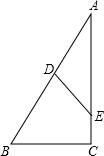 如图,∠A+∠B=90°,点D在线段AB上,点E在线段AC上.
如图,∠A+∠B=90°,点D在线段AB上,点E在线段AC上. 已知点A,B,C,D的坐标分别是A(0,0),B(3,4),C(-2,6),D(-3,2).
已知点A,B,C,D的坐标分别是A(0,0),B(3,4),C(-2,6),D(-3,2). 如图,抛物线y1=-x2+2x+3与直线y2=4x交于A,B两点.
如图,抛物线y1=-x2+2x+3与直线y2=4x交于A,B两点.