题目内容
2.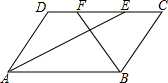 如图,在?ABCD中,AB=8cm,AD=5cm,∠BAD的平分线交CD于点E,∠ABC的平分线交CD于点F,则线段EF的长2cm.
如图,在?ABCD中,AB=8cm,AD=5cm,∠BAD的平分线交CD于点E,∠ABC的平分线交CD于点F,则线段EF的长2cm.
分析 由于平行四边形的两组对边互相平行,又AE平分∠BAD,由此可以推出所以∠BAE=∠DAE,则DE=AD=5;同理可得,CF=CB=5,而EF=CF+DE-DC,由此可以求出EF长.
解答 解:∵AE平分∠BAD,
∴∠BAE=∠DAE,
又∵AD∥CB,
∴∠EAB=∠DEA,
∴∠DAE=∠AED,
则AD=DE=5;
同理可得,CF=CB=5.
∴EF=DE+CF-DC=5+5-8=2.
故答案为:2.
点评 此题主要考查了角平分线的定义、平行四边形的性质、平行线的性质等知识,关键注意找出线段之间的关系:EF=DE+CF-DC.

练习册系列答案
相关题目
11.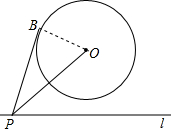 如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点.若PB切⊙O于点B,则PB的最小值是( )
如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点.若PB切⊙O于点B,则PB的最小值是( )
 如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点.若PB切⊙O于点B,则PB的最小值是( )
如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点.若PB切⊙O于点B,则PB的最小值是( )| A. | $\sqrt{13}$ | B. | $\sqrt{5}$ | C. | 3 | D. | 2 |
12.将6.38×10-4化为小数是( )
| A. | 0.000638 | B. | 0.0000638 | C. | 0.00638 | D. | 0.0638 |
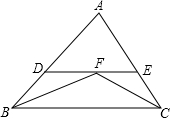 如图所示,∠ABC、∠ACB的平分线相交于点F,过点F作DE∥BC交AB于D,交AC于E.若AB=9cm,AC=8cm,则△ADE的周长是多少?
如图所示,∠ABC、∠ACB的平分线相交于点F,过点F作DE∥BC交AB于D,交AC于E.若AB=9cm,AC=8cm,则△ADE的周长是多少?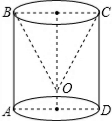 如图,圆柱体内挖去一个与它不等高的圆锥,锥顶O到AD的距离为1,∠OCD=30°,OC=4,则挖去圆锥后的表面积是(16+8$\sqrt{3}$)π.
如图,圆柱体内挖去一个与它不等高的圆锥,锥顶O到AD的距离为1,∠OCD=30°,OC=4,则挖去圆锥后的表面积是(16+8$\sqrt{3}$)π.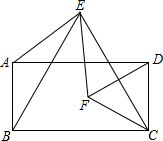 已知:如图所示,四边形ABCD是矩形,分别以BC、CD为一边作等边△EBC和等边△FCD,点E在矩形上方,点F在矩形内部,连接AE、EF.
已知:如图所示,四边形ABCD是矩形,分别以BC、CD为一边作等边△EBC和等边△FCD,点E在矩形上方,点F在矩形内部,连接AE、EF.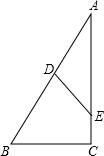 如图,∠A+∠B=90°,点D在线段AB上,点E在线段AC上.
如图,∠A+∠B=90°,点D在线段AB上,点E在线段AC上.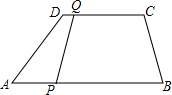 如图,在梯形ABCD中,CD∥AB,且CD=6cm,AB=9cm,P、Q分别从A、C同时出发,P以1cm/s的速度由A向B运动,Q以2cm/s的速度由C向D运动.则2或3秒时,直线QP将四边形ABCD截出一个平行四边形.
如图,在梯形ABCD中,CD∥AB,且CD=6cm,AB=9cm,P、Q分别从A、C同时出发,P以1cm/s的速度由A向B运动,Q以2cm/s的速度由C向D运动.则2或3秒时,直线QP将四边形ABCD截出一个平行四边形.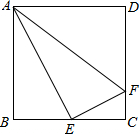 如图,在正方形ABCD中,点E为BC的中点,CF=$\frac{1}{4}$CD,连接AE、AF、EF.设CF=a
如图,在正方形ABCD中,点E为BC的中点,CF=$\frac{1}{4}$CD,连接AE、AF、EF.设CF=a