题目内容
20.若-$\frac{a}{3}$≤-$\frac{a}{2}$,则a一定满足( )| A. | a>0 | B. | a<0 | C. | a≥0 | D. | a≤0 |
分析 根据$\frac{1}{3}<\frac{1}{2}$,所以-$\frac{1}{3}$>-$\frac{1}{2}$,因为-$\frac{a}{3}$≤-$\frac{a}{2}$,根据不等式的基本性质,所以a≤0.
解答 解:∵$\frac{1}{3}<\frac{1}{2}$,
∴-$\frac{1}{3}$>-$\frac{1}{2}$,
∵-$\frac{a}{3}$≤-$\frac{a}{2}$
∴a≤0,
故选:D.
点评 本题主要考查了不等式的基本性质.“0”是很特殊的一个数,因此,解答不等式的问题时,应密切关注“0”存在与否,以防掉进“0”的陷阱.
不等式的基本性质:
(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.

练习册系列答案
相关题目
9.已知一组数据10,8,9,x,4的众数是8,那么这组数据的中位数是( )
| A. | 4 | B. | 8 | C. | 9 | D. | 10 |
 如图,点M在正方形ABCD的对角线BD上.求证:AM=CM.
如图,点M在正方形ABCD的对角线BD上.求证:AM=CM.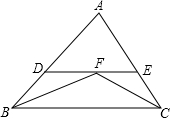 如图所示,∠ABC、∠ACB的平分线相交于点F,过点F作DE∥BC交AB于D,交AC于E.若AB=9cm,AC=8cm,则△ADE的周长是多少?
如图所示,∠ABC、∠ACB的平分线相交于点F,过点F作DE∥BC交AB于D,交AC于E.若AB=9cm,AC=8cm,则△ADE的周长是多少? ,这时的时刻应是12:01.
,这时的时刻应是12:01.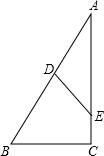 如图,∠A+∠B=90°,点D在线段AB上,点E在线段AC上.
如图,∠A+∠B=90°,点D在线段AB上,点E在线段AC上.