题目内容
4.等腰直角三角形的外接圆半径的长为1,则其内切圆半径的长$\sqrt{2}$-1.分析 由于直角三角形的外接圆半径是斜边的一半,由此可求得等腰直角三角形的斜边长,进而可求得两条直角边的长;然后根据直角三角形内切圆半径公式求出内切圆半径的长即可.
解答 解:∵等腰直角三角形外接圆半径为1,
∴此直角三角形的斜边长为2,两条直角边分别为$\sqrt{2}$,
∴它的内切圆半径为:r=$\frac{1}{2}$($\sqrt{2}$+$\sqrt{2}$-2)=$\sqrt{2}$-1.
故答案为:$\sqrt{2}$-1.
点评 本题考查了三角形的外接圆和三角形的内切圆,等腰直角三角形的性质,要注意直角三角形内切圆半径与外接圆半径的区别:直角三角形的内切圆半径:r=$\frac{1}{2}$(a+b-c);(a、b为直角边,c为斜边)直角三角形的外接圆半径:R=$\frac{1}{2}$c.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
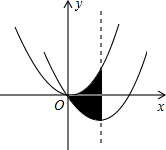 如图,在平面直角坐标系中,抛物线y=$\frac{1}{2}$x2经过平移得到抛物线y=$\frac{1}{2}$x2-2x,求其对称轴与两段抛物线所围成的阴影部分的面积.
如图,在平面直角坐标系中,抛物线y=$\frac{1}{2}$x2经过平移得到抛物线y=$\frac{1}{2}$x2-2x,求其对称轴与两段抛物线所围成的阴影部分的面积.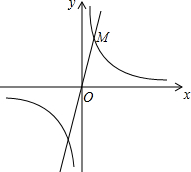 如图,在平面直角坐标系xOy中,反比例函数y=$\frac{4}{x}$的图象与正比例函数y=kx的图象的一个交点为M(1,b).
如图,在平面直角坐标系xOy中,反比例函数y=$\frac{4}{x}$的图象与正比例函数y=kx的图象的一个交点为M(1,b).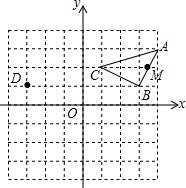 如图,在平面直角坐标系中,点D的坐标是(-3,1),点A的坐标是(4,3).
如图,在平面直角坐标系中,点D的坐标是(-3,1),点A的坐标是(4,3). 如图所示,直线AB与双曲线y=$\frac{k}{x}$交于A,B两点,直线AB与x、y坐标轴分别交于C,D两点,连接OA,若OA=2$\sqrt{13}$,tan∠AOC=$\frac{2}{3}$,B(-3,m)
如图所示,直线AB与双曲线y=$\frac{k}{x}$交于A,B两点,直线AB与x、y坐标轴分别交于C,D两点,连接OA,若OA=2$\sqrt{13}$,tan∠AOC=$\frac{2}{3}$,B(-3,m)