题目内容
19.解不等式组:$\left\{\begin{array}{l}{2(1-x)+3>0}\\{\frac{3x-1}{2}+1≥x}\end{array}\right.$.分析 分别求出每一个不等式的解集,根据口诀:大小小大中间找,确定不等式组的解集.
解答 解:解不等式2(1-x)+3>0,得:x<$\frac{5}{2}$,
解不等式$\frac{3x-1}{2}$+1≥x,得:x≥-1,
∴不等式组的解集是$-1≤x<\frac{5}{2}$.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8. 2015年6月28日,“合福高铁”正式开通,对南平市的旅游产业带来了新的发展机遇.某旅行社抽样调查了2015年8月份该社接待来南平市若干个景点旅游的人数,并将调查结果绘制成如下两幅不完整的统计图表,请根据图表信息回答下列问题:
2015年6月28日,“合福高铁”正式开通,对南平市的旅游产业带来了新的发展机遇.某旅行社抽样调查了2015年8月份该社接待来南平市若干个景点旅游的人数,并将调查结果绘制成如下两幅不完整的统计图表,请根据图表信息回答下列问题:
(1)此次共调查400人,并补全条形统计图;
(2)由上表提供的数据可以制成扇形统计图,则“天成奇峡”所对扇形的圆心角为75.6°;
(3)该旅行社预计今年8月份将要接待来以上景点的游客约2 500人,根据以上信息,请你估计去“九曲溪”的游客大约有多少人?
 2015年6月28日,“合福高铁”正式开通,对南平市的旅游产业带来了新的发展机遇.某旅行社抽样调查了2015年8月份该社接待来南平市若干个景点旅游的人数,并将调查结果绘制成如下两幅不完整的统计图表,请根据图表信息回答下列问题:
2015年6月28日,“合福高铁”正式开通,对南平市的旅游产业带来了新的发展机遇.某旅行社抽样调查了2015年8月份该社接待来南平市若干个景点旅游的人数,并将调查结果绘制成如下两幅不完整的统计图表,请根据图表信息回答下列问题:| 景点 | 频数 (人数) | 频率 |
| 九曲溪 | 116 | 0.29 |
| 归宗岩 | 0.25 | |
| 天成奇峡 | 84 | 0.21 |
| 溪源峡谷 | 64 | 0.16 |
| 华阳山 | 36 | 0.09 |
(2)由上表提供的数据可以制成扇形统计图,则“天成奇峡”所对扇形的圆心角为75.6°;
(3)该旅行社预计今年8月份将要接待来以上景点的游客约2 500人,根据以上信息,请你估计去“九曲溪”的游客大约有多少人?
8.下列计算正确的是( )
| A. | -$\frac{x}{y}$÷2y=-$\frac{x}{2}$ | B. | a2b•$\frac{a}{2b}$=$\frac{{a}^{3}}{2}$ | C. | (a2-b2)•$\frac{1}{b-a}$=a+b | D. | m3n2÷$\frac{{n}^{2}}{m}$•m=m3 |
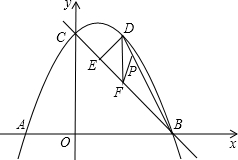 已知:如图,直线y=-x+2与x轴交于B点,与y轴交于C点,A点坐标为(-1,0).
已知:如图,直线y=-x+2与x轴交于B点,与y轴交于C点,A点坐标为(-1,0).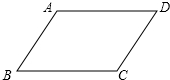 如图,已知?ABCD.
如图,已知?ABCD.
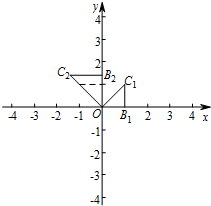 已知:如图,在平面直角坐标系xOy中,点B1,C1的坐标分别为(1,0),(1,1).将△OB1C1绕原点O逆时针旋转90°,再将其各边都扩大为原来的m倍,使OB2=OC1,得到△OB2C2;将△OB2C2绕原点O逆时针旋转90°,再将其各边都扩大为原来的m倍,使OB3=OC2,得到△OB3C3.如此下去,得到△OBnCn.
已知:如图,在平面直角坐标系xOy中,点B1,C1的坐标分别为(1,0),(1,1).将△OB1C1绕原点O逆时针旋转90°,再将其各边都扩大为原来的m倍,使OB2=OC1,得到△OB2C2;将△OB2C2绕原点O逆时针旋转90°,再将其各边都扩大为原来的m倍,使OB3=OC2,得到△OB3C3.如此下去,得到△OBnCn.